なぜスペクトルのピークが2つ？
前々回・前回とスペクトルを求める例として使用していた信号x(t)ですが、図1に示すように、信号形状自体は正弦波（sin波）と同じで、ただ開始の起点位置が異なっていて、純粋な正弦波に比べて開始が先行している（専門的には「位相が進んでいる」という）だけの波形です。
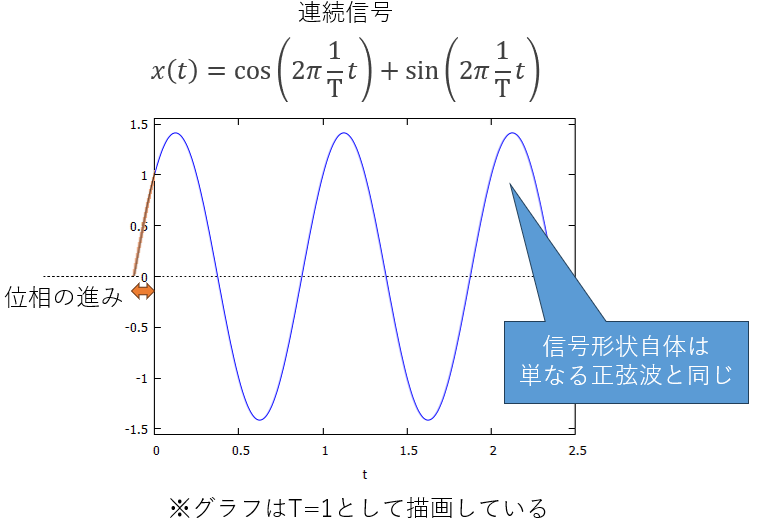
図1：例題信号は位相の進んだ正弦波
周波数スペクトルというのは、どの周波数の正弦波が混ざっているかを示す情報なので、（位相がずれているとはいえ）単一正弦波であるx(t)のスペクトルは、1本線だけ（＝1つの正弦波のみで構成）見えそうなものです。
それなのに、離散フーリエ変換を用いて求めたスペクトルには図2のように2つのピークが見えました（図2では振幅スペクトルを示していますが、位相スペクトルやパワースペクトルも同様です）。これはいったいどういうことなのでしょうか。
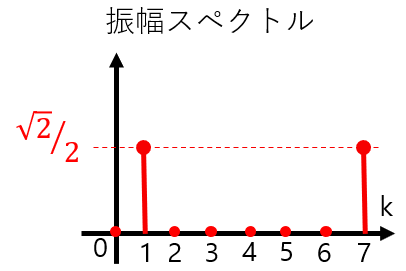
図2：例題信号の振幅スペクトル（再掲）
負の周波数と折り返し
（離散ではない）フーリエ変換で得られたスペクトルは、縦軸を中心に左右対称で負の周波数が存在していましたが（フーリエ変換編2参照）、離散フーリエ変換で得たスペクトルにも同様に負の周波数が存在します。そして離散フーリエ変換は、入力信号を離散信号にする代償として、スペクトルが周期的になっているという特徴があります（フーリエ変換編3参照）。ですので、図2に示した振幅スペクトルは、もっとズームアウトして「引き」でみると図3のような姿をしています。
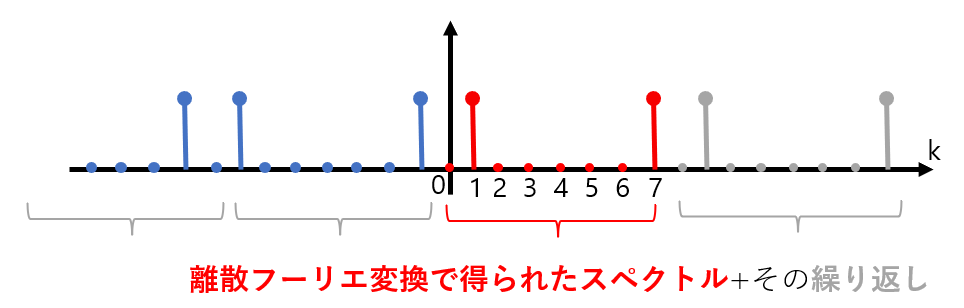
図3：「引き」で見たスペクトル
フーリエ変換と同じように、縦軸を中心としたスペクトルに着目すると、k=4,5,6のスペクトルは、負の周波数に相当する情報であることがわかります（図4）。
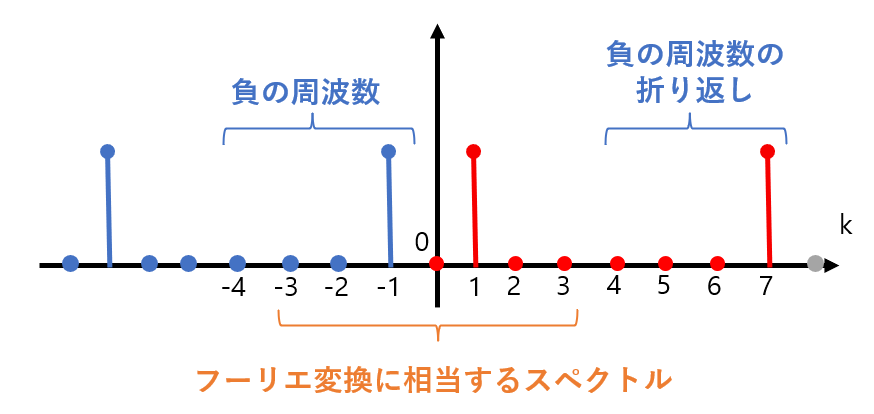
図4：負の周波数とその折り返し
このように、スペクトルが周期的になったことで負の周波数があたかも正の周波数であるように見えることを「折り返し」と言います。8点DFTを計算すると8個のスペクトル情報が得られますが、実はそのうちの約半分（4～6）は負の周波数が折り返したものであり、実用上の意味を持ちません（図5）。ただしこの説明はかなり乱暴なものですので、コラムも合わせて参照してください。
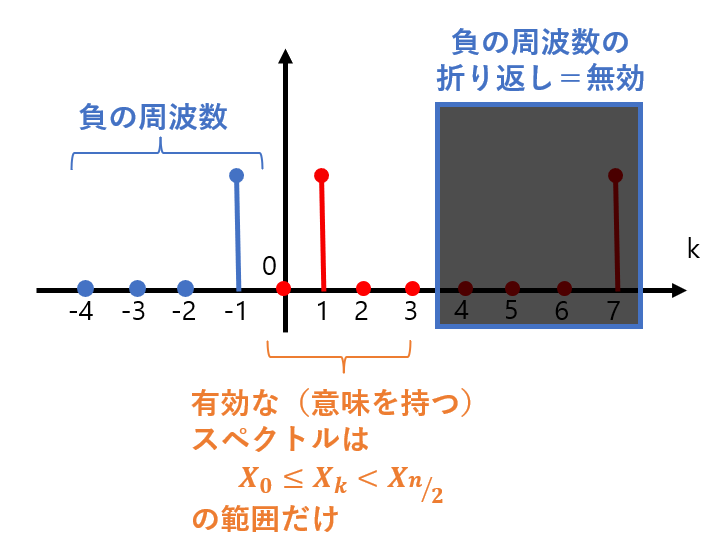
図5：有効なスペクトル
ちょっと余談：負の周波数は本当に無意味なのか？
本文では説明をすっきりさせるために「負の周波数成分（及びその折り返し）が、物理的な意味を持たない」と書きましたが、もう少し正確には、この部分を無視できるための条件があります。
本稿におけるフーリエ級数展開（及びその仲間）の説明は、「電気信号や音などの、物理的な信号」を対象としていることと「元信号が三角関数sin波（正弦波）・cos波（余弦波）の重ね合わせで表現されている」ことを前提とし、フーリエ級数展開（及びその仲間）を使用して「元信号がどのようなsin波（正弦波）・cos波（余弦波）の重ね合わせで構成されているかを求める」ことを目的としていました。この条件の限りでは、負の周波数成分（及びその折り返し）は無視することができます。なぜならば、三角関数に負の周波数を取り入れたとしても、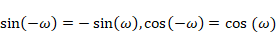
という関係があるため、結局正の周波数で同じ情報が表現できてしまいます。
一方、sin, cos関数と複素指数関数はオイラーの公式により相互に変換できる関係があることをすでに説明しました。元信号を「（三角関数ではなく）複素指数関数の重ね合わせ」としてとらえる場合、周波数の正負は複素指数関数の回転方向を表す情報になるため、負の周波数成分も意味を持ちます。
Xkと周波数
離散フーリエ変換で得られたスペクトルは横軸がkになっているので、これを物理的な意味（周波数）に読み替えましょう。
サンプリング周波数を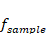
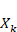
とした場合、離散フーリエ変換で得られたスペクトル
は、周波数
に相当します。
本連載では前提として、信号のサンプリング間隔（サンプリング周期）を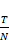
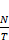
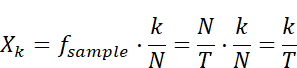
としているので、サンプリング周波数はその逆数、すなわち
ですから、
となります。先に示した図1のグラフではT=1として描画しているので、この場合
の周波数に対応する成分となります。離散フーリエ変換の結果、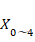
の中で
だけにピークが立っているので、この信号は1[Hz]の正弦波であると解釈できます。
スペクトルとナイキスト周波数の関係
「準備編2：アナログ信号とデジタル信号」において、サンプリング周波数の半分を「ナイキスト周波数」と呼ぶという話をしました。
アナログ信号をサンプリングする時は、ナイキスト周波数未満の信号しか正常に復元できないのですが、スペクトルを見るとその理由がわかります。
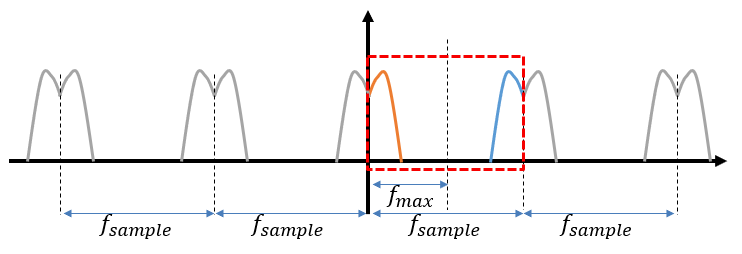
図6：スペクトルとサンプリング周波数・ナイキスト周波数の関係
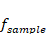
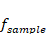
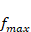
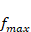
図6は、離散フーリエ変換で得られたスペクトル（赤枠内）が、無限に繰り返されている様子を表しています。赤枠の右端を周波数で表現すると、これはサンプリング周波数に相当します。（でk=Nの時）そして縦軸との中点がナイキスト周波数
に相当します。上図では、得られたスペクトル（赤枠）をナイキスト周波数で切り、その右側（負の周波数：青部分）を捨てれば、求めているスペクトル（正の周波数：オレンジ色部分）が取得できます。
ところが、ナイキスト周波数を超える信号成分が含まれていると、スペクトルは図7のようになります。
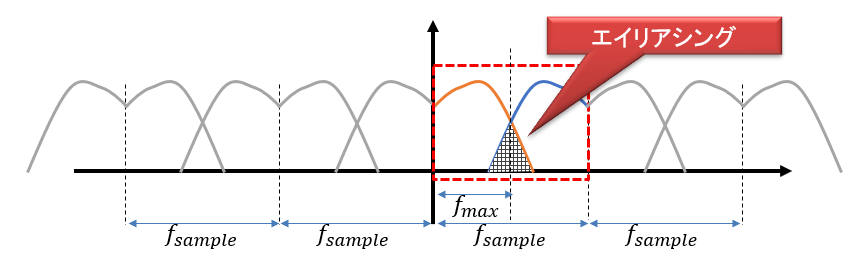
図7：エイリアシング
正の周波数（オレンジ色部分）と負の周波数：青部分が重なり合ってしまって、求めているスペクトル（正の周波数：オレンジ色部分）だけを取り出すことができなくなってしまいます。この現象及びこの現象によって生じた雑音を「エイリアシング」または「折り返し雑音」といいます。
Maximaを用いて離散フーリエ変換
Maximaを使って、離散フーリエ変換の別の事例を解いてみましょう。（Wolfram Alphaで解くためには回転因子行列の入力が大変なのでMaximaを使用します）
関数
を図8のように離散化し、8点DFTを行います。1[Hz]の正弦波と、振幅半分で2[Hz]の正弦波を混合したものです。
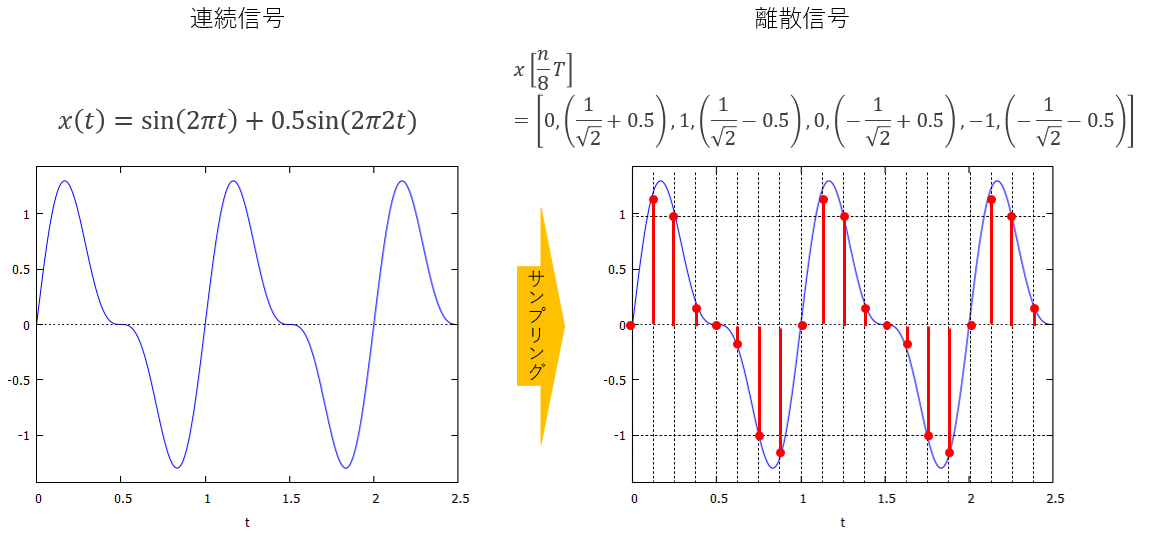
図8：例題信号2のサンプリング
まず、連続信号の関数x(t)を定義した後、サンプリングした信号を並べた入力信号ベクトルを作ります。信号の周期1[sec]を8等分してサンプリングしています（図9）。
図9：例題信号2のサンプリング（Maxima）
次に8点DFT用の回転因子行列を作ります。まず公式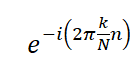
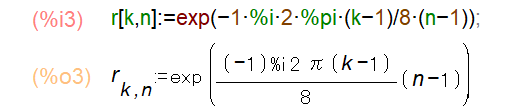
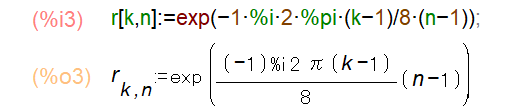
を使って、2次元配列を作ります。ただし公式のk,nは0から始まる想定なのに対して、Maximaの引数k,nは1から始まるため、(k-1),(n-1)として使用しています（図10）。
図10：回転因子行列の作成1（Maxima）
作成した2次元配列を行列に変換します（図11）。
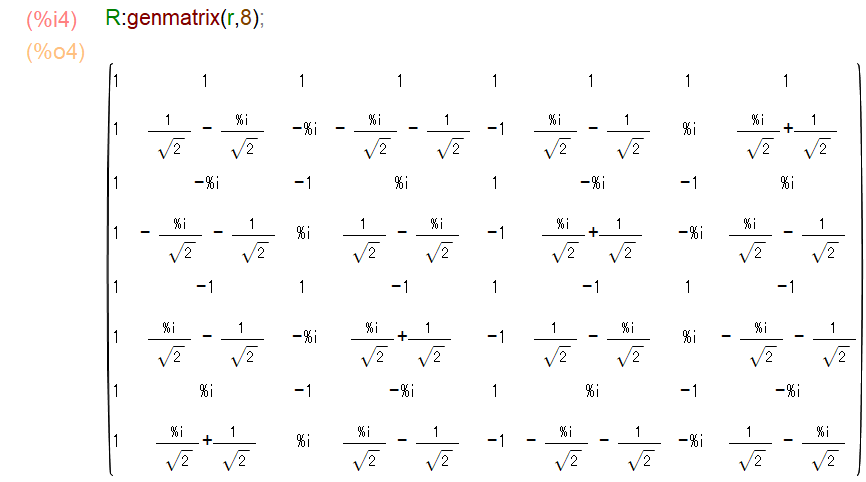
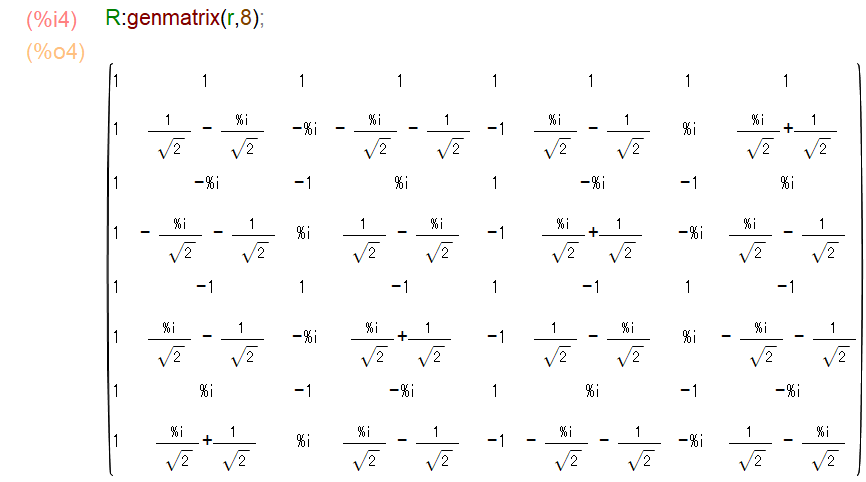
図11：回転因子行列の作成2（Maxima）
離散フーリエ変換を行うため
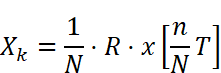
の計算をします。Maximaではアスタリスク（*ただしMaximaの画面上は・と表示される）はスカラーの積であって、行列の積は.（ピリオド）で書かなければならない事に注意してください（図12）。
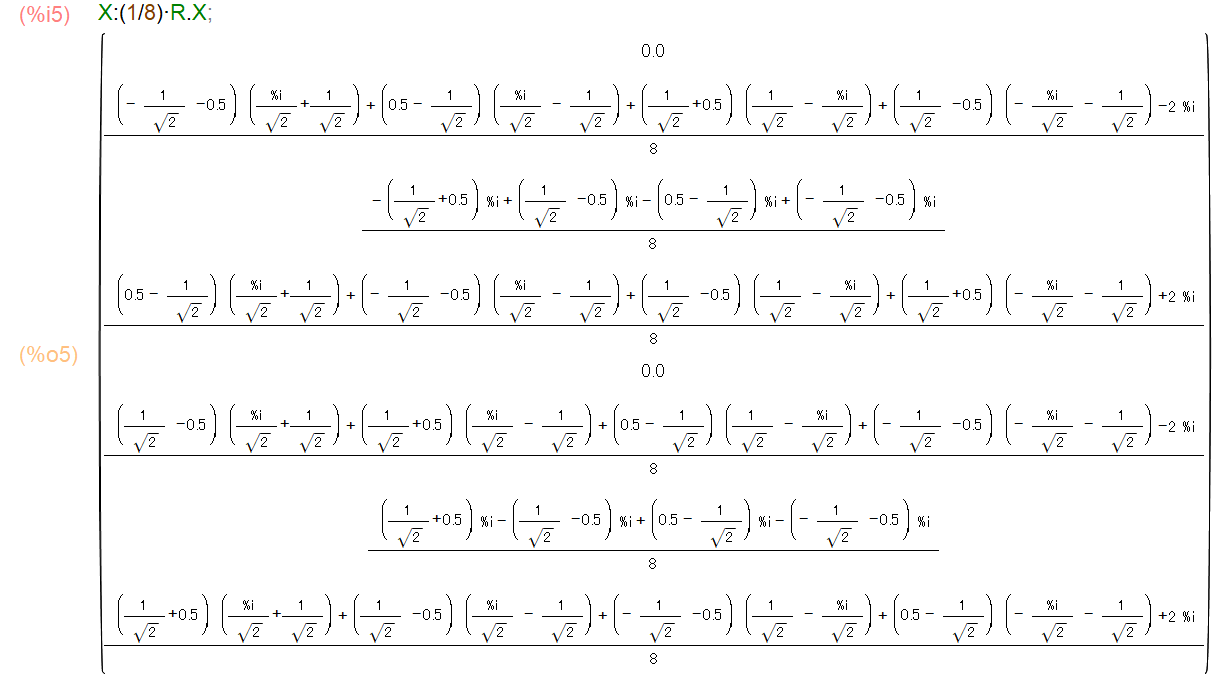
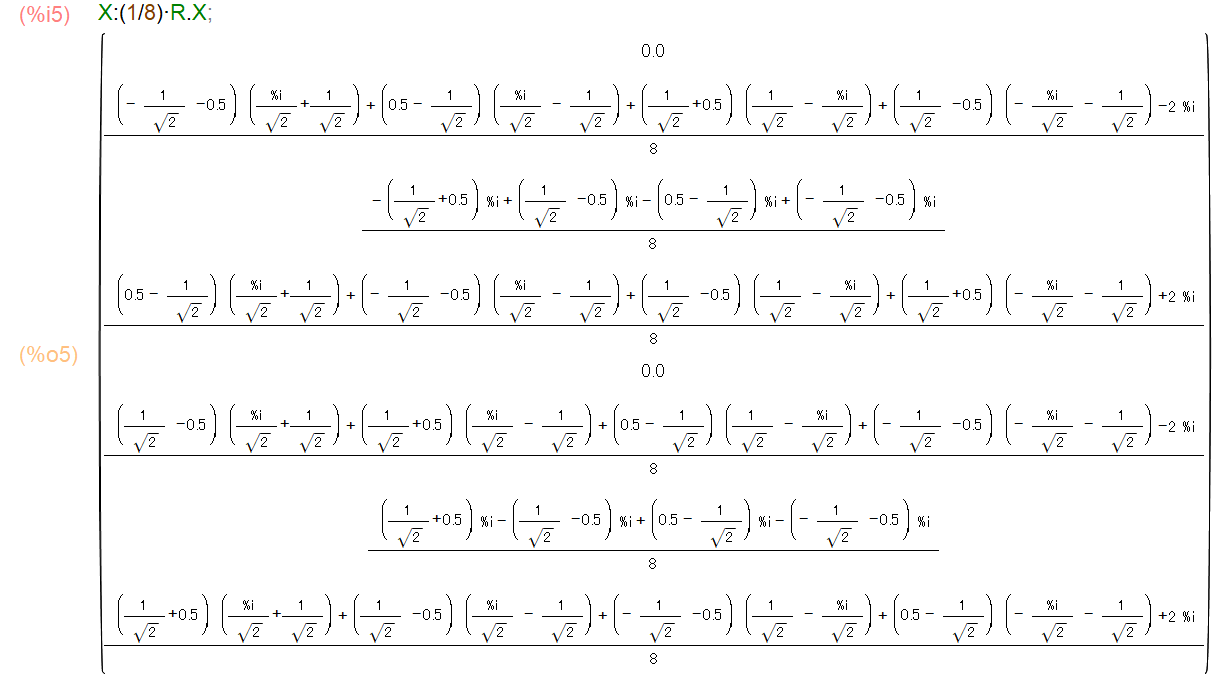
図12：例題信号2 離散フーリエ変換の計算（Maxima）
かなりややこしい結果が出てきてしまいましたが、これはMaximaが計算しきれていないだけです。全ての成分を展開するexpand命令で計算させます（図13）。
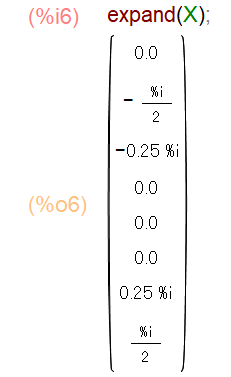
図13：例題信号2 スペクトル関数の展開計算（Maxima）
各成分の絶対値を求めると振幅スペクトルが得られます（図14）。
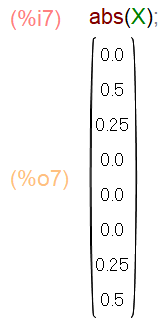
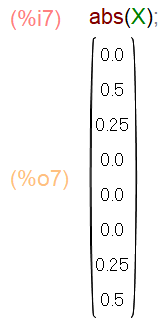
図14：例題信号2の振幅スペクトルを求める（Maxima）
絶対値の2乗を求めるとパワースペクトルが得られます（図15）。
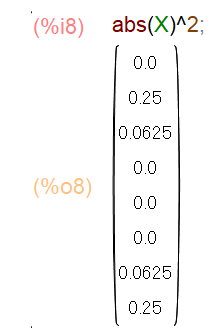
図15：例題信号2のパワースペクトルを求める（Maxima）
carg関数を用いて偏角を求めると位相スペクトルが得られますが、そのままではよくわからない値が出てきてしまいます（図16）。
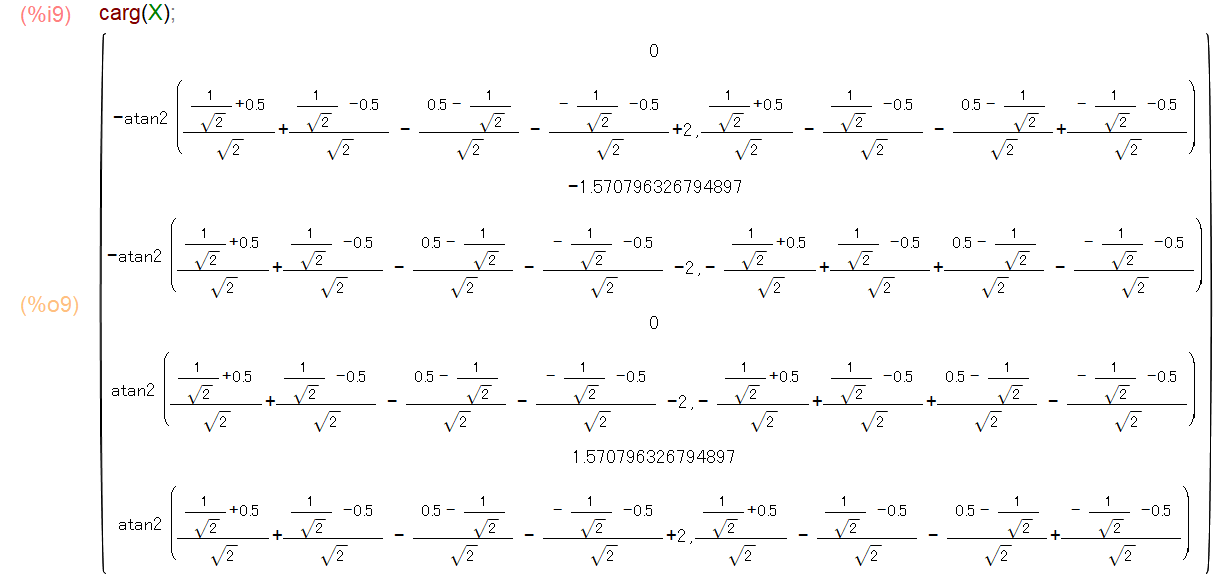
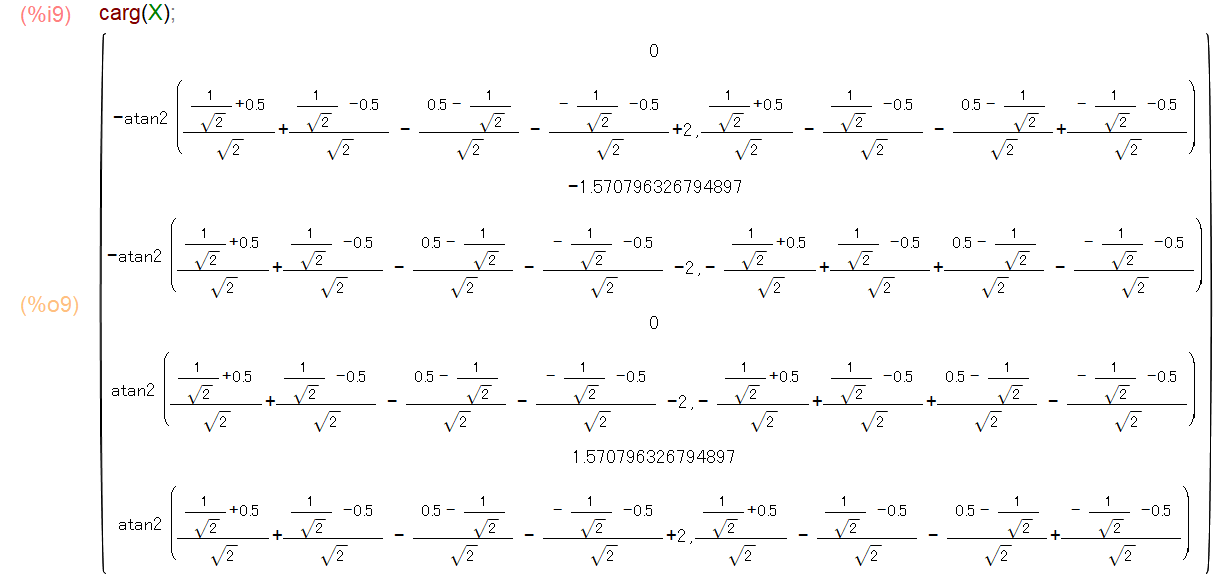
図16：例題信号2の位相スペクトルを求める1（Maxima）
そこでfloat関数を通して、具体的な実数値にすると次のようになります（図17）。
図17：例題信号2の位相スペクトルを求める2（Maxima）
スペクトルを描くと図18のようになります。不要な後ろ半分のスペクトルを無視して、k=0～3までの値をみると、振幅スペクトルから、1[Hz]と2[Hz]の成分が2:1の比率で混ざっていることがわかります。
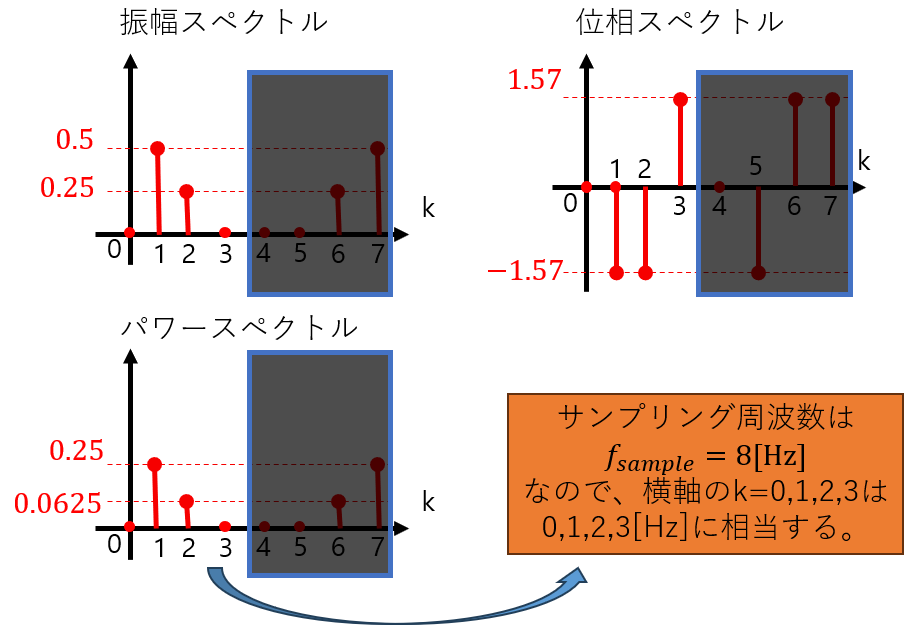
図18：例題信号2の各スペクトル
もうひとつ、別の事例を計算してみましょう。
関数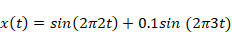
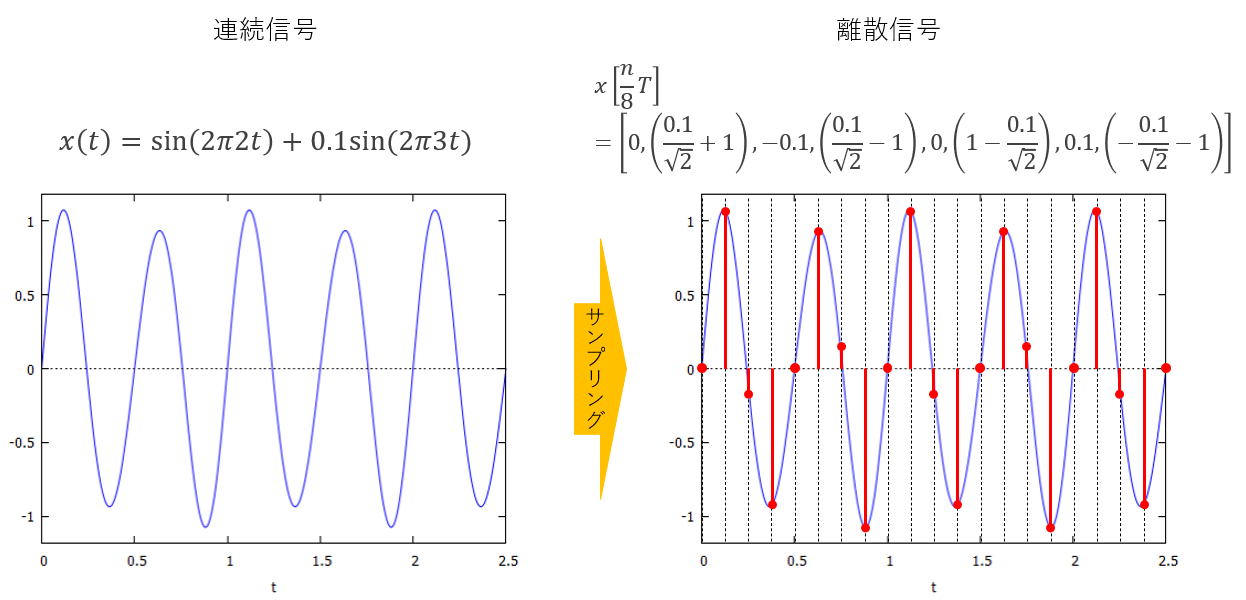
を図19のように離散化し、8点DFTを行います。2[Hz]の正弦波と、その10%の振幅で3[Hz]の正弦波を混合したものです。
図19：例題信号3のサンプリング
連続信号の関数x(t)を定義した後、サンプリングした信号を並べた入力信号ベクトルを作ります。信号の周期1[sec]を8等分してサンプリングしています（図20）。
図20：例題信号2のサンプリング（Maxima）
今回も8点DFTなので、回転因子行列の作り方は先ほどと全く同じです（図21）。
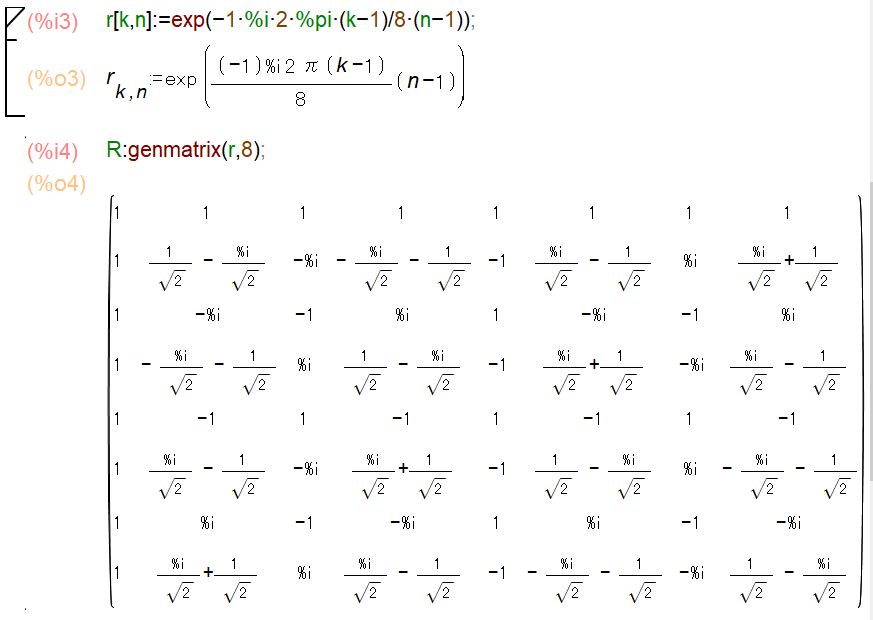
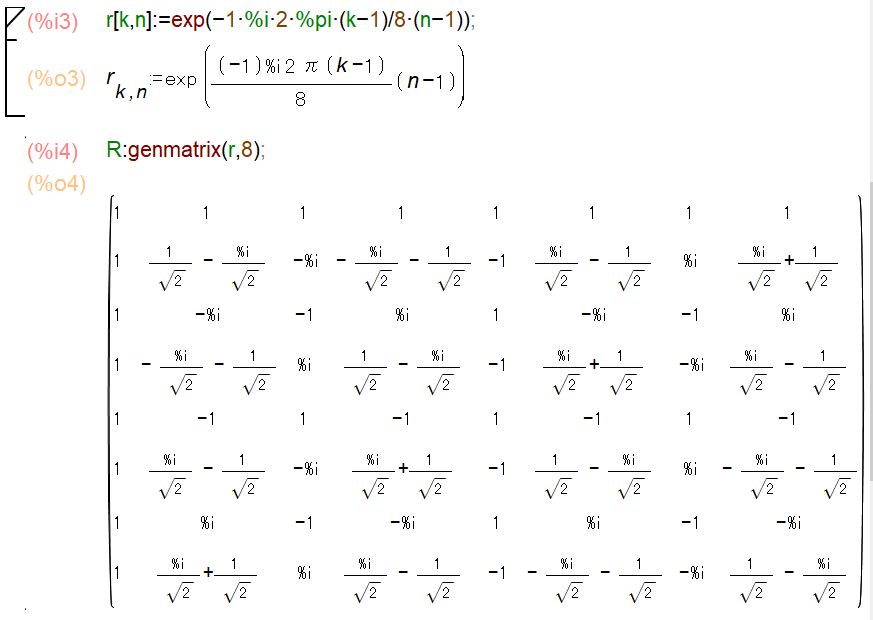
図21：回転因子行列の作成（Maxima）
ここから離散フーリエ変換を計算します（図22）。
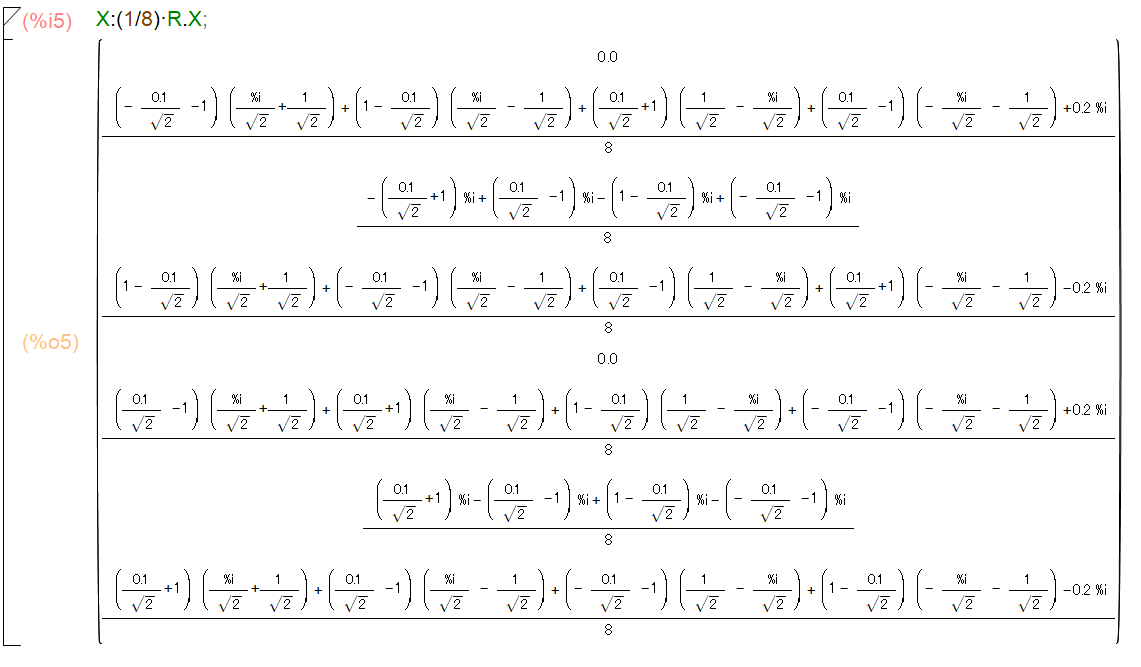
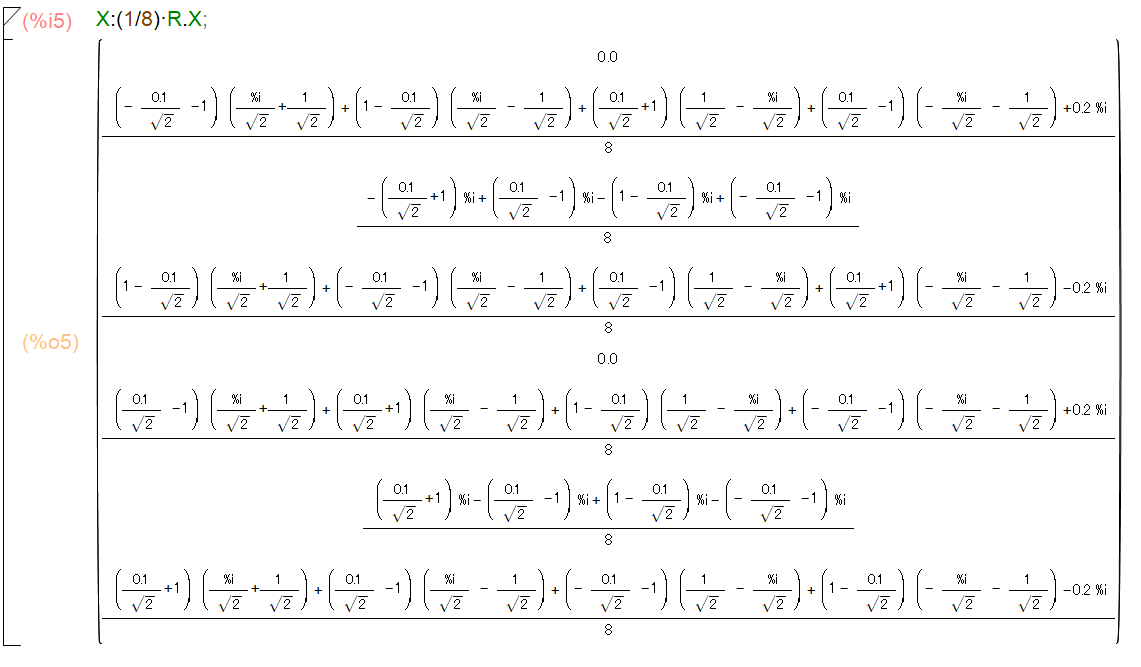
図22：例題信号3 離散フーリエ変換の計算（Maxima）
得られたスペクトル関数をexpand命令で展開すると図23のようになります。
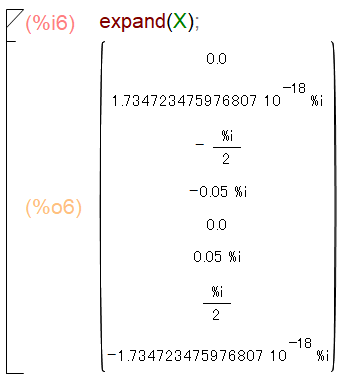
図23：例題信号3 スペクトル関数の展開計算（Maxima）
絶対値を求めて振幅スペクトルを、それを2乗してパワースペクトルを求めます（図24）。なおX[1]とX[7]は10の-18乗や10の-36乗がかかっている極めて小さい値なので、実質0と考えて良いでしょう。
図24：例題信号3の振幅スペクトルとパワースペクトルを求める（Maxima）
cargを用いて位相スペクトルを求めます（図25）。
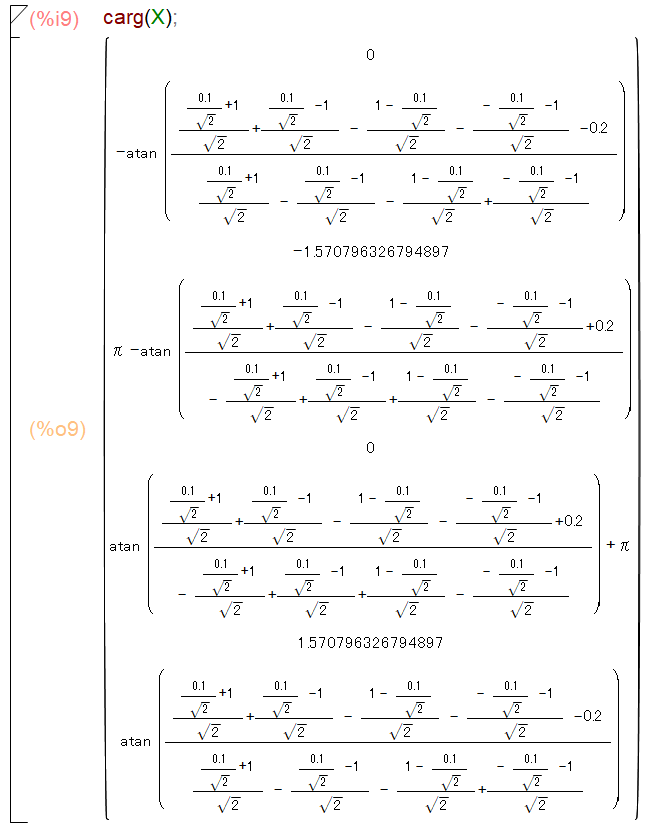
図25：例題信号3の位相スペクトルを求める１（Maxima）
とんでもなくややこしい値が出てくるので、float命令で実数にします（図26）。
図26：例題信号3の位相スペクトルを求める2（Maxima）
スペクトルを描くと次のようになります。不要な後ろ半分のスペクトルを無視して、k=0～3までの値をみると、振幅スペクトルから、2[Hz]と3[Hz]の成分が10:1の比率で混ざっていることがわかります（図27）。
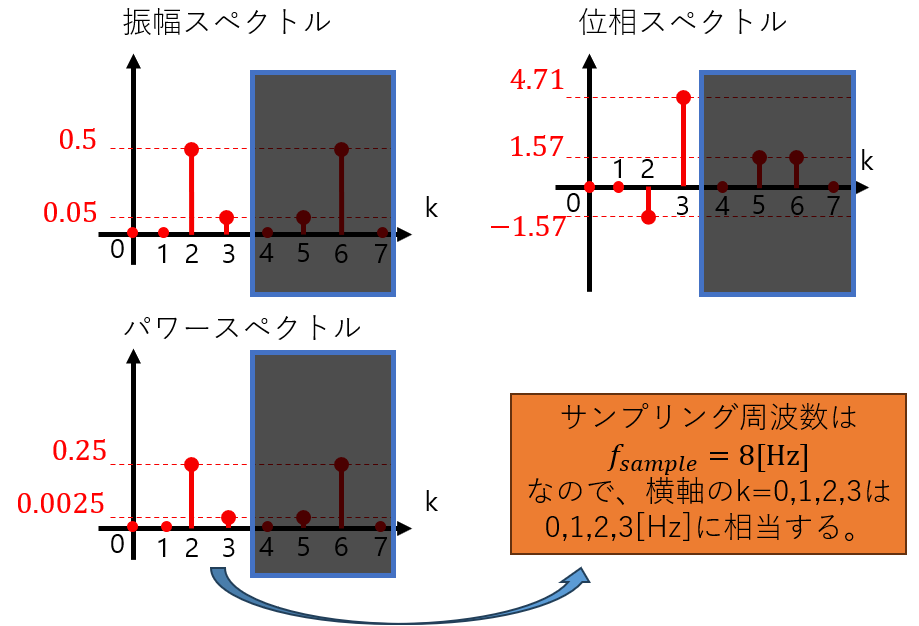
図27：例題信号3の各スペクトル
これで、離散フーリエ変換が使えるようになりました。次からはいよいよ、離散フーリエ変換を本連載の到達目標である高速フーリエ変換（FFT）に発展させていきます。
こちらも是非
“もっと見る” ブログ
はじめての耐量子暗号
量子コンピューティングはさまざまな面で明るい未来のために期待される技術である反面、その演算能力をセキュリティ上の攻撃に使われることを考えると、既存の暗号技術にとって深刻な脅威でもあります。
Arm®対応のWindows IoT OS 【Windows IoT on Arm】を評価ボードで動かしてみる
組み込み機器向けOS、Windows 10/11 IoT Enterprise(以下Windows IoT)がサポートするArmプラットフォームが拡大しています。Windows IoT on Armは、Windows IoTのメリットそのまま、より低コストで低消費電力というArmならではのメリットもございます
【フーリエ変換を試してみる：フーリエ変換編2】イメージでしっかりつかむ信号処理〜基礎から学ぶFFT〜
前回はフーリエ変換の意味と、複素フーリエ係数を求める式からフーリエ変換の式が得られる事を説明しました。今回は実践編という事でフーリエ変換を試してみたいと思います。