FFTに舞う蝶
「蝶のように舞い、蜂のように刺す（Float like a Butterfly, Sting like a Bee）」は名ボクサーであるモハメド・アリのファイトスタイルを表現した有名なフレーズです。実はFFTの中にもたくさんの蝶が舞っています。FFTの中に舞う蝶が何を意味しているのか、を理解しましょう。
前回の記事で、8点DFT（8×8の回転因子行列）を4つの2×2回転因子行列に分割できるという事を説明しました。その計算過程は、図1のように1枚の絵で表すことができます（ただし先頭の1/Nは省略しています）。
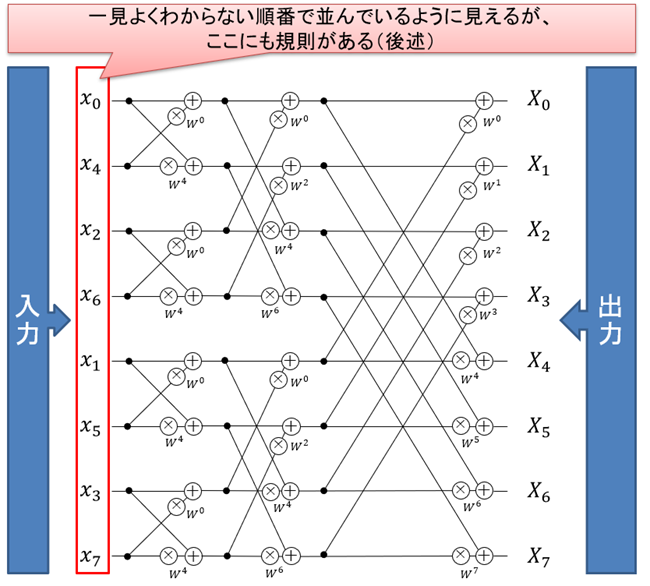
図1：8点FFTの図解
図1は入力信号を左端に置き、左から右へ流れながら処理を行います。途中にある丸印は演算を表します、＋は左側から入ってきた値を「加算」して右側に送ります。×は左から入った値に、横に書いてある回転因子をかけ算して右側に送ります。
この図が正しく計算を表しているかどうか確認してみましょう。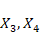
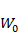
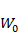
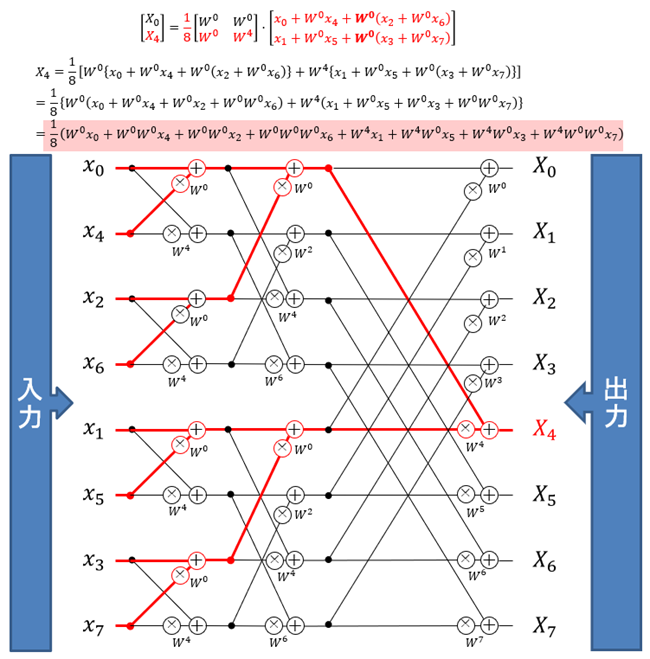
の計算過程を示したものを図.2と図3に示します。左から右に赤線をたどりつつ、ピンク色に塗った数式と比べてみて下さい。なお式と図を見比べたときに回転因子の
の数が合っていませんが、は「１」なので、何度かけても、かけなくても、値に変化がなく、事実上問題はありません。
図2：X4の計算過程を図示
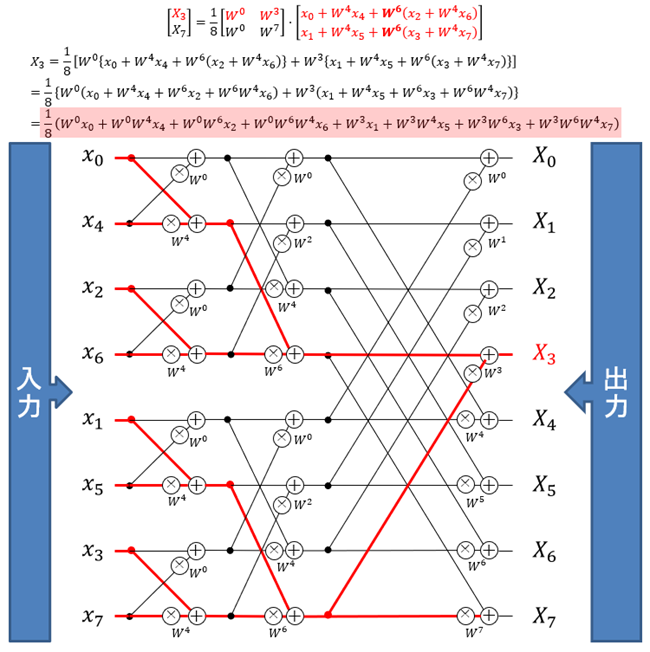
図3：X3の計算過程を図示
この流れ図の基本構造は図4の形をしています。見た目が蝶に見えることから、「バタフライ演算」という名前がついています。
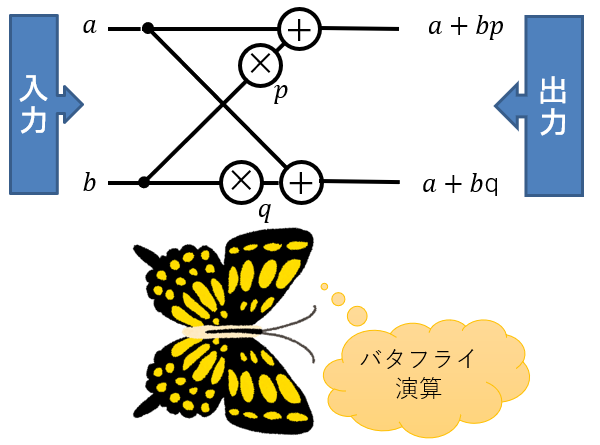
図4：バタフライ演算
図1を観察すると、規則的な構造が見て取れます。線のたすき掛け交差は左から順に1本・2本・4本…と２のべき乗で増えていきます。横線も1本先（隣）同士をつなぎ、2本先をつなぎ、4線先をつなぎ…とやはり２のべき乗で増えていきます。また係数のかけ算は必ず「合流地点の下側」に入ります。係数の大きさは左から右に向かって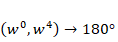
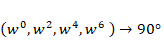
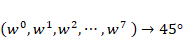
ずつ、
ずつ、
ずつ、と、回転角度が半分ずつ変化しています。
これらは、前回の記事で説明したように8点FFTを2つの4点FFT→4つの2点FFTと分割していく事を意味しています。無駄を省きながら、大きなFFTを2点FFTまで分解して処理を行っているのです（図5）。
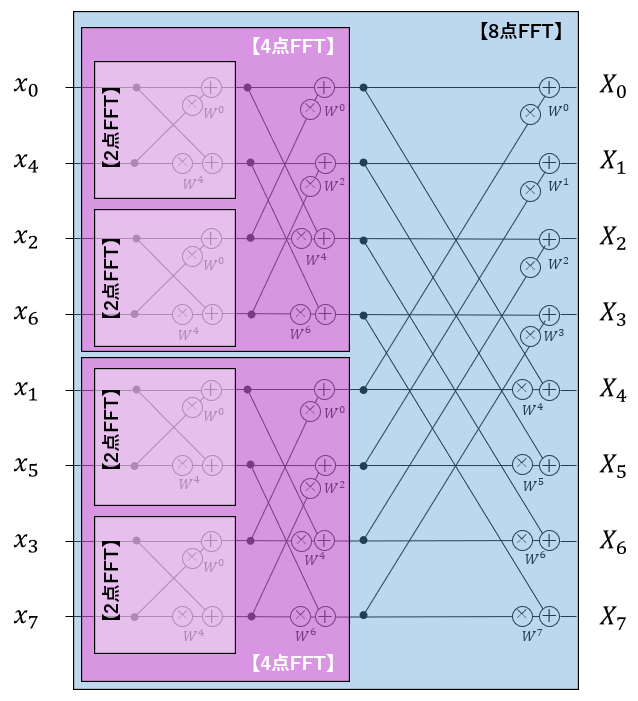
図5：FFTの階層構造
ビットリバーサル
入力信号の係数は0,4,2,6,1,5,3,7という不思議な並びをしています。これは「ビットリバーサル順という独特の並びになっています。図6のように、添え字を一度2進数で書いた後、ビットの並びを逆順にすることで求められます。（2進数がよくわからない人は、後述の付録を参照のこと）
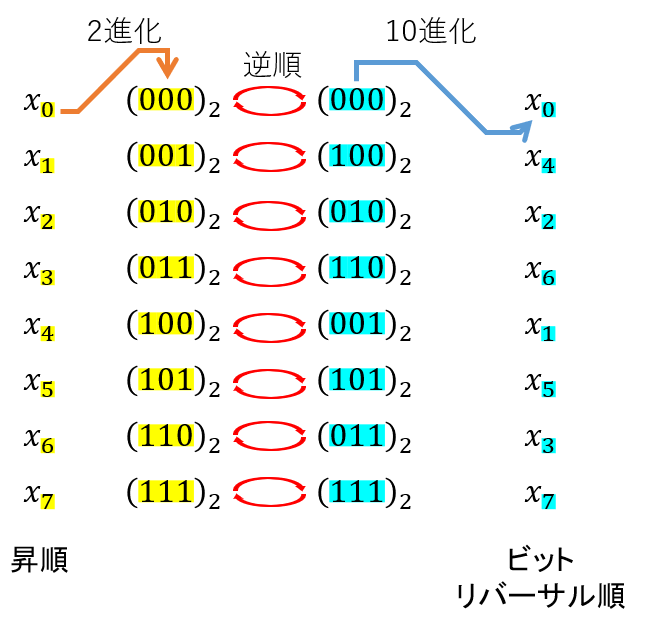
図6：ビットリバーサル順の求め方
ここまでの図では出力信号が0～7と並ぶように描いているため、入力信号がビットリバーサル順になっています。逆に入力信号の係数が0～7と並ぶように図を書くと、出力（スペクトル関数）側の係数がビットリバーサル順になります。
ここまで理解すれば、あとは16点でも32点でも1024点でもFFTを行うことができます。長らく連載を続けてきましたが、ついに高速フーリエ変換を理解するところまで到達しました。ここまでお読みいただいた皆様、お疲れ様でした。しかし連載はもう少し続きます。次回からは、より実践的に高速フーリエ変換を使うためのノウハウを学んでいきます。
付録 2進数（ついでに16進数）を理解する
スーパーの値札に（１１００）と書いてあれば、私たちはこれを「千百」と理解します。これは私たちが普段、数字を「10進数」として理解しているためです。
10進数の重要なポイントを図7に示します。1つのケタに0から9までの10種類の記号を（数字）を使用して数値を表示します。0から順に1,2,3…とカウントアップしていき、下位ケタが9まで使い切ると上位（左隣）のケタが1つ増えます。そのため、各ケタは一・十・百・千…と10倍ずつ異なる重みをもちます。小学校の算数で習う「位（くらい）」という概念と同じです。図7下線部に「10」という数値が登場していることに注目して下さい。
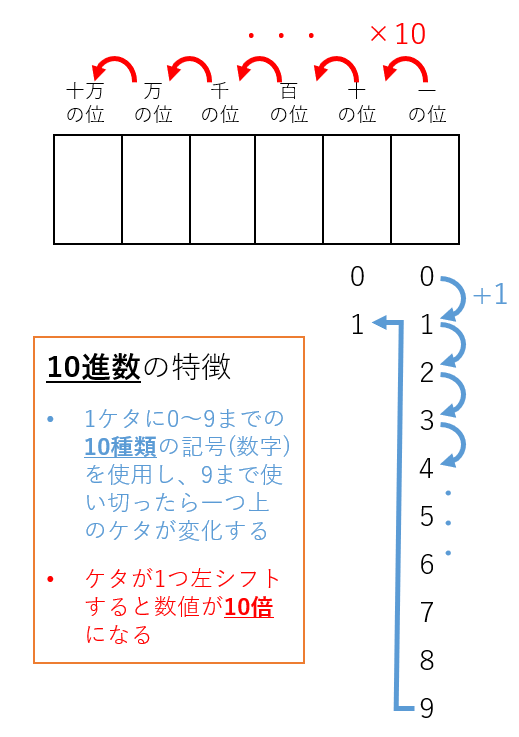
図7：10進数の特徴
図7の下線部を全て「２」に書き換えると、2進数の説明になります（図8）。1つのケタに0から1までの2種類の記号を（数字）を使用して数値を表示します。0から順に1までカウントアップしていき、下位ケタが1まで使い切ると上位のケタが1つ増えます。そのため、各ケタは一・二・四・八…と2倍ずつ異なる重みをもちます。
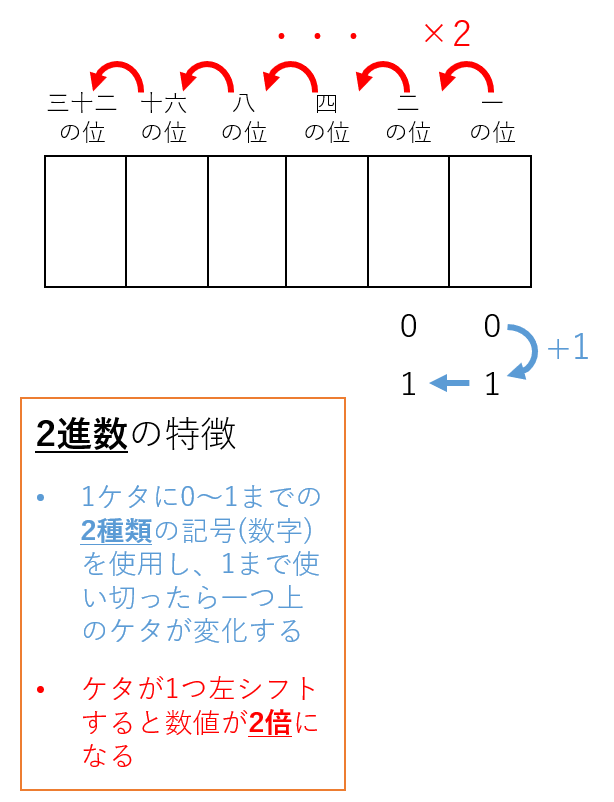
図8：2進数の特徴
コンピュータの世界では16進数もよく使用します（図9）。1つのケタに0から9の数字、さらにA～Fまでのアルファベットを加え、計16種類の記号を（数字）を使用して数値を表示します。0から順に1,2,3…とカウントアップしていき、下位ケタがFまで使い切ると上位のケタが1つ増えます。そのため、各ケタは一・十六・・二百五十六…と16倍ずつ異なる重みをもちます。
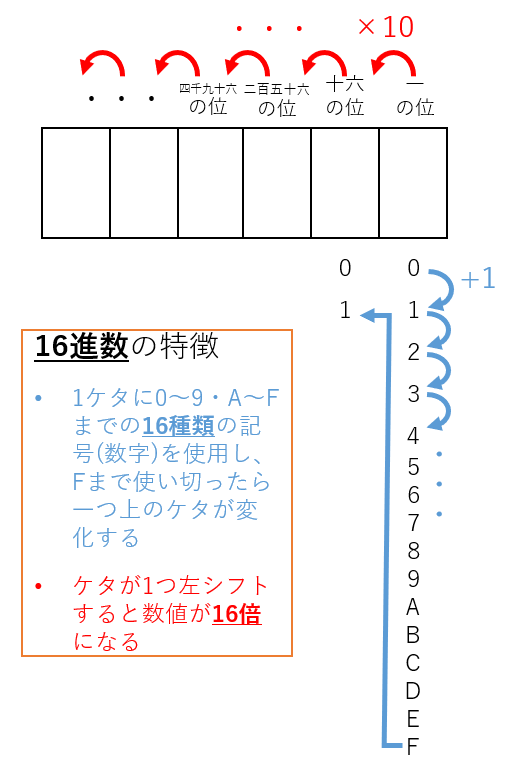
図9：16進数の特徴
0～30までの整数を10進数・2進数・16進数で表現すると図10のようになります。
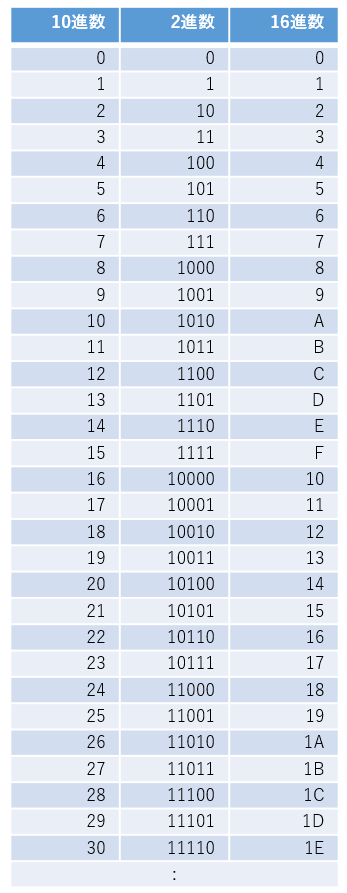
図10：10進数・2進数・16進数対応表
こちらも是非
“もっと見る” ブログ
【離散フーリエ変換を読み解く：フーリエ変換編4】イメージでしっかりつかむ信号処理〜基礎から学ぶFFT〜
複雑に見えますが、離散フーリエ変換の式と複素フーリエ級数の式（係数を求める式）とを照らし合わせると、複素フーリエ級数を自然な形で離散信号用に書き換えたものであることがわかります。図１のように両者を並べて、5つのポイント（①～⑤）に注目しながら照らし合わせてみましょう。
はじめての耐量子暗号
量子コンピューティングはさまざまな面で明るい未来のために期待される技術である反面、その演算能力をセキュリティ上の攻撃に使われることを考えると、既存の暗号技術にとって深刻な脅威でもあります。
Arm®対応のWindows IoT OS 【Windows IoT on Arm】を評価ボードで動かしてみる
組み込み機器向けOS、Windows 10/11 IoT Enterprise(以下Windows IoT)がサポートするArmプラットフォームが拡大しています。Windows IoT on Armは、Windows IoTのメリットそのまま、より低コストで低消費電力というArmならではのメリットもございます