現実的な分析を目指そう
ここまでの解説は全て、「波形の全体」かつ「入力信号の繰り返し周期切れ目ピッタリで始まり、ピッタリで終わる信号」を対象として分析を行ってきました。この条件では、一番ノイズがなくきれいな分析結果が得られますが、現実的な分析としては無理があります。
【問題1】時間変化を追えない
《おはよう》という音が「おはよう」という文字として認識できるのは、《お》《は》《よ》《う》の各文字が固有の周波数特性を持っているからです。しかし《おはよう》という一連の音声波形全体をまとめて周波数分析してしまうと、それぞれの違いがわからなくなってしまいます(図1)。
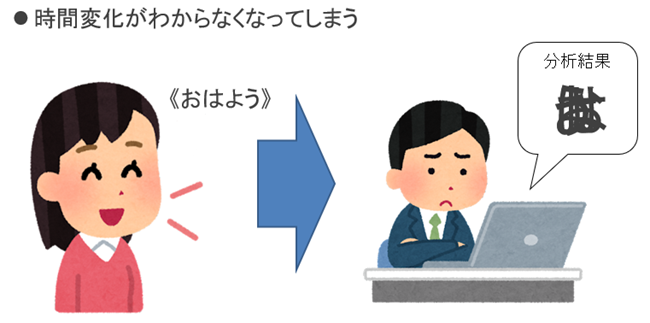
図1:全体をまとめて分析すると時間変化がわからなくなる
【問題2】周期の切れ目がわからないため不連続点が生じる
離散フーリエ変換は、入力信号が永遠に繰り返される前提で計算を行います。
信号が繰り返し周期ピッタリで始まりピッタリで終わると、繰り返しがなめらかにつながるので良い分析結果が得られます。これがずれてしまうと繰り返し部分で不連続点が生じて、これが分析のノイズになります。
繰り返し周期ピッタリの分析範囲を定めるためには、元の信号の周期を知る必要があります。周期を知るという事は信号の基本周波数を知ることと同義なので、周波数分析をするために前提条件として事前に周波数を知っていなければいけないという矛盾が生じてしまいます。
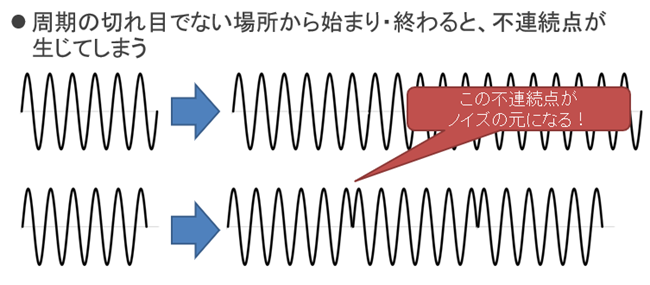
図2:繰り返し部分で不連続点が生じるとノイズになる
短時間フーリエ変換(STFT)
「【問題1】時間変化を追えない」に対処するために考えられた手法が「短時間フーリエ変換」(Short-Time Fourier Transform : STFT)というものです(フーリエ変換と言っていますが、(連続)フーリエ変換に限っているわけではありません。そういう意味ではShort-Time Fourier Analysis と言った方が適切なように思いますが、慣習的にこう呼んでいます)。
大層な名前がついていますがやっている事は非常に単純です。入力信号全体を分析するのではなく、一定時間ごとに区切り、切り出す場所(分析対象)をずらしながら、それぞれに周波数分析を行います。これにより周波数成分の時間変化がわかります。
図で具体的にイメージしましょう。図3に示した波形は低・中・高の3種類の周波数が順番に現れていますが、これを全てまとめて分析してしまうと3つの周波数成分がまとめて出てきてしまい、時間変化がわかりません。
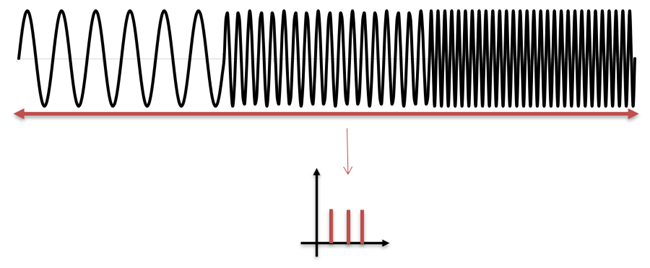
図3:3つの周波数が順に現れる信号を、まとめて分析
そこで、短い時間間隔で入力信号を切り出し、切り出す場所をずらしながら繰返し分析する(スライディングウィンドウ)ことで、周波数の時間変化が見えるようになります。
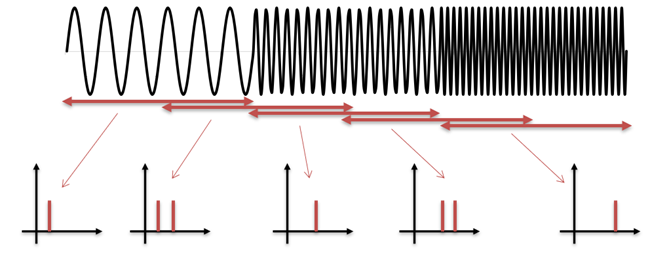
図4:3つの周波数が順に現れる信号を、短い時間に区切って分析
STFTを行う場合はウィンドウ幅とオーバーラップ幅を設定する必要があります(図5)。ウィンドウ幅は1回に分析する区間の長さ、オーバーラップ幅は隣同士の分析区間をどれだけ重ねるか示す値になります。
ウィンドウ幅とオーバーラップ幅の調整は大変重要なポイントになります。
ウィンドウ幅を小さくすると細かい時間変化がわかるようになる(時間分解能が高くなる)一方で、細かい周波数の違いが識別できなくなる(周波数分解能が落ちる)ことになります。ウィンドウ幅を広げれば細かい周波数の違いが識別できる(周波数分解能が高くなる)一方で細かい時間変化がわからなくなります(時間分解能が低くなる)。
オーバーラップ幅を大きくとる(分析区間の重なりを広くとる)と時間変化を追いやすくなりますが全体の分析数が増えて処理が遅くなります。オーバーラップ幅を小さくとる(分析区間があまり重ならないようにする)と分析数が減って処理が軽くなりますが時間変化を追いにくくなってしまいます(ここでいう「時間変化を追いやすく/追いにくくなる」という表現は「時間分解能が高く/低くなる」ととらえることもできますが、上述したウィンドウ幅の変化による時間分解能の変化とは意味が違うため、表現をわけました)。
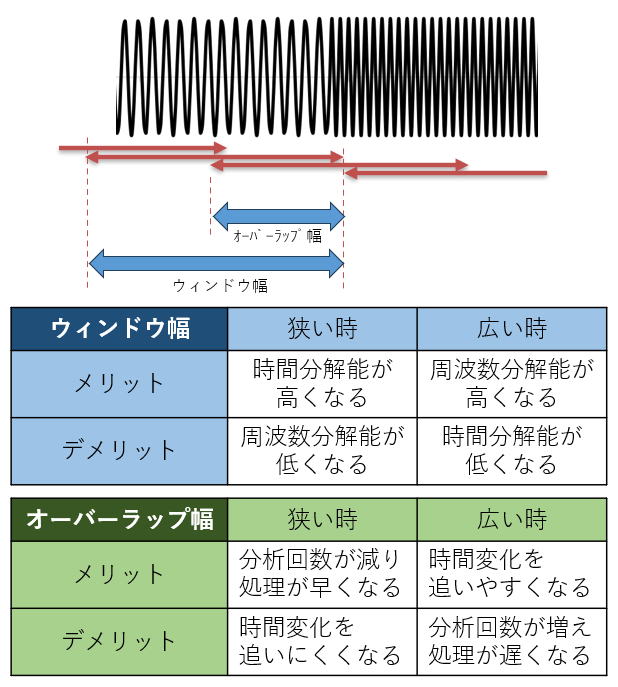
図5:ウィンドウ幅とオーバーラップ幅
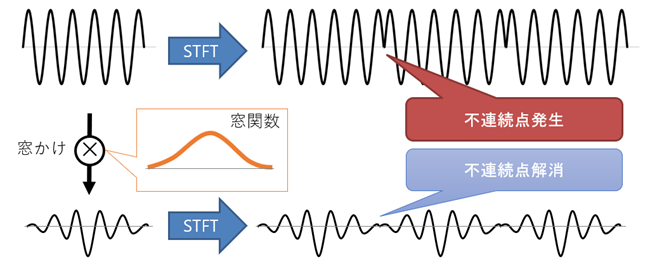
窓かけ・窓関数
「【問題2】周期の切れ目がわからないため不連続点が生じる」に対処するために考えられた手法が「窓かけ」(Windowing)というものです。STFTのために入力信号から分析区間を切り出すと、頭とお尻の両端部分で不連続点が生じてしまうので、「中心部分がほぼ1で、両端がほぼ0」の関数(窓関数)をかけ算し、分析区間の両端がほぼ0になるように信号を変形させる手法です。
窓かけは分析区間両端での不連続点発生を抑えることができる反面、信号を変形させてしまうので、元々信号が持っていた本来の周波数成分と、分析によって得られる周波数成分に違いが出てしまうという副作用を持ちます。しかし一般的には副作用による問題に比べると不連続点が発生するデメリットの方が大きいと考えられるため、窓かけが使用されます。
窓関数は「中心部分がほぼ1で、両端がほぼ0」という条件さえ満たしていれば様々な形状が使用できます。それぞれ特性が微妙に異なるため、用途に応じて適切な窓関数を選ぶことが望ましいです。しかしどのようにすれば適切な窓関数を選べるかというのは難しい問題です。代表的な窓関数を5つ紹介します。それぞれの図には2つの波形が示されています。左は窓の形状、右は10.45[Hz]の正弦波に窓をかけたものです。
【窓関数1】矩形(くけい)窓・方形(ほうけい)窓
矩形・方形は共に長方形という意味の言葉です。窓「関数」と言いつつも実態はただの1、つまり入力信号に対して分析区間を切り出すだけで他は「何もしない」窓になります。「両端がほぼ0」という特性を満たしていないので「窓関数」と呼ぶのもおかしな気がしますが、他の窓関数と比較した議論を行うときに、「矩形窓をかける(=窓をかけない)」という表現を使うことがあります。また信号の性質や分析の意図によって、意図的に矩形窓を使用する場合もあります。
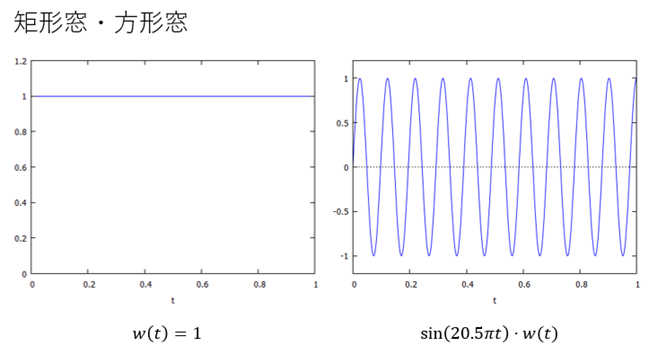
図6:矩形窓・方形窓
【窓関数2】ガウス窓・ガウシアン窓
ガウス関数またはガウシアン関数と呼ばれる関数を使用した窓です。σの値を変える事で山の鋭さを変える事が出来ます(ちなみに、統計学を学ぶと登場する「正規分布」はガウス関数の特殊例です)。厳密には左右へ無限に伸びる関数のため、実用的にはどこかで計算を打ち切って使用する必要があります。そのため打ち切りに伴うノイズが発生することがあります。
ガウス窓を使用したSTFTは「ガボール変換」と呼ばれる事もあり、画像処理などで使用されます。
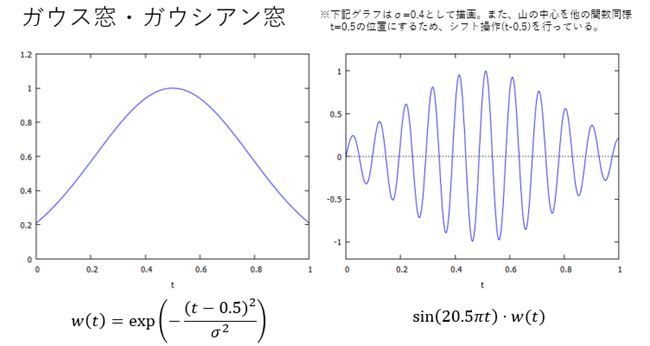
図7:ガウス窓・ガウシアン窓
【窓関数3】ハニング窓
コサインを使用した窓関数で、最もよく利用される窓関数です。
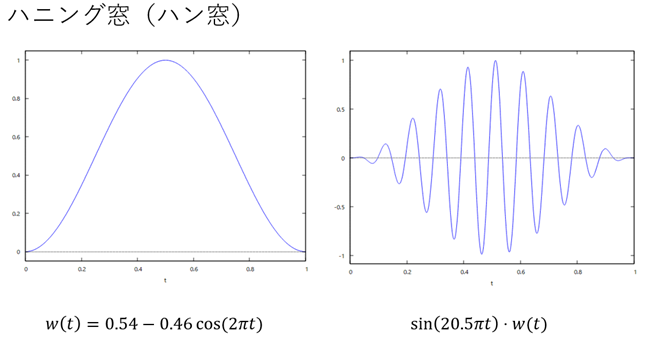
図8:ハニング窓
【窓関数4】ハミング窓
ハニング窓に似ているが、係数が異なります。周波数選択性が良い特徴があります。
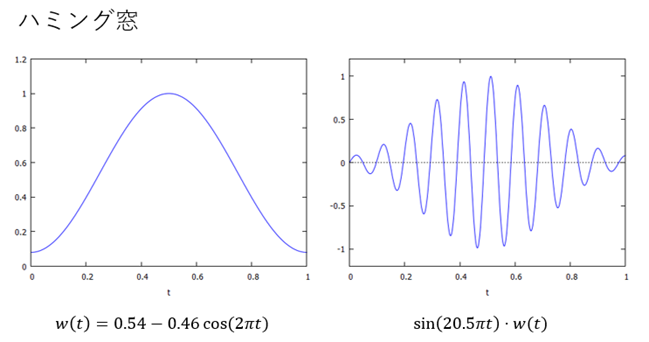
図9:ハミング窓
【窓関数5】ブラックマン窓
ハミング窓と同じくコサインを使用した窓関数です。ハミング窓に比べると周波数選択性は劣りますが、ハミング窓と比べると窓の両端がしっかりゼロ近くまで落ちていることがわかります。
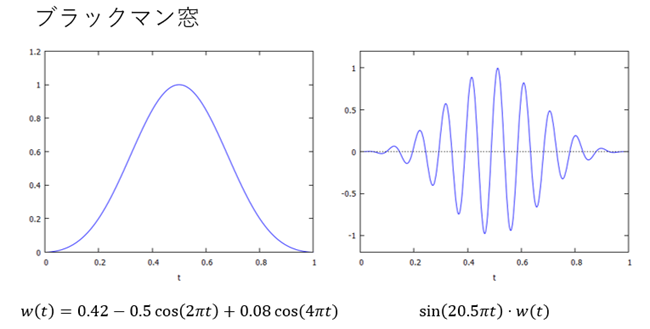
図10:ブラックマン窓
次回は、FFT分析ツールを使用しながら、実際に音を分析するハンズオンを行います。
こちらも是非
“もっと見る” ブログ
はじめてのセキュア転送〜組み込み向けMCUでセキュア転送を動かしてみる〜
セキュアファイル転送の基本機能について説明します。また、理解を助けるために実際のMCUでセキュアファイル転送を行う簡単なサンプルプログラムを動かしてみたいと思います。
【離散フーリエ変換を実現してくれる行列:フーリエ変換編5】イメージでしっかりつかむ信号処理〜基礎から学ぶFFT〜
離散フーリエ変換の対象となっている離散入力信号が8個あるので、これに対する離散フーリエ変換を「8点の離散フーリエ変換」とか、さらに短縮して「8点DFT」と言ったりします。同様に前回の例題は4点DFTといいます。
【離散フーリエ変換を読み解く:フーリエ変換編4】イメージでしっかりつかむ信号処理〜基礎から学ぶFFT〜
複雑に見えますが、離散フーリエ変換の式と複素フーリエ級数の式(係数を求める式)とを照らし合わせると、複素フーリエ級数を自然な形で離散信号用に書き換えたものであることがわかります。図1のように両者を並べて、5つのポイント(①~⑤)に注目しながら照らし合わせてみましょう。