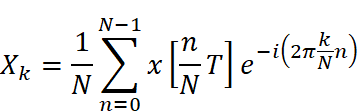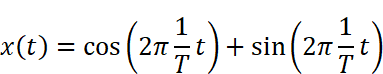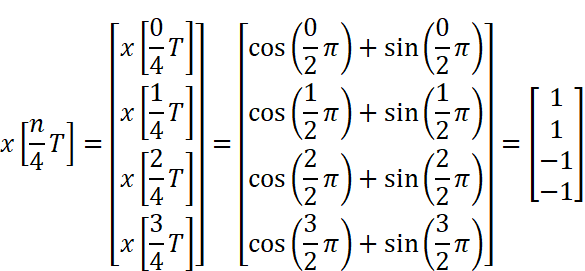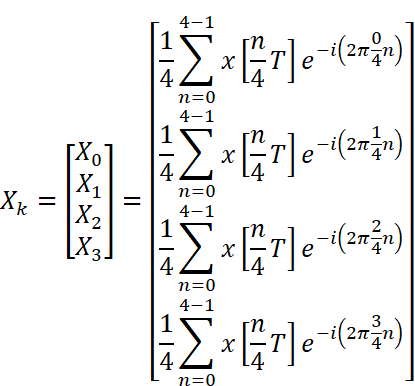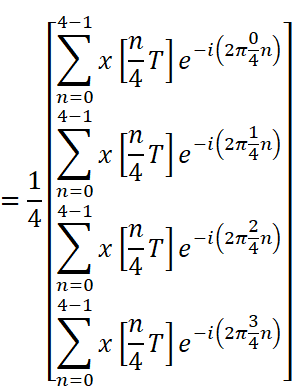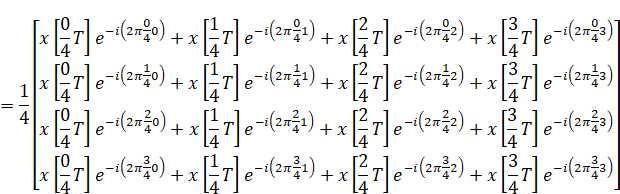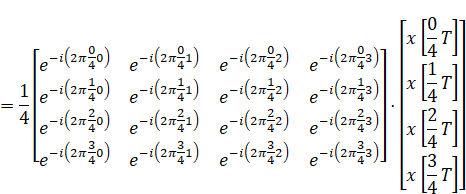離散フーリエ変換の成り立ち
離散信号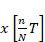
に対する離散フーリエ変換は以下の式で定義されます。
複雑に見えますが、離散フーリエ変換の式と複素フーリエ級数の式（係数を求める式）とを照らし合わせると、複素フーリエ級数を自然な形で離散信号用に書き換えたものであることがわかります。図１のように両者を並べて、5つのポイント（①～⑤）に注目しながら照らし合わせてみましょう。
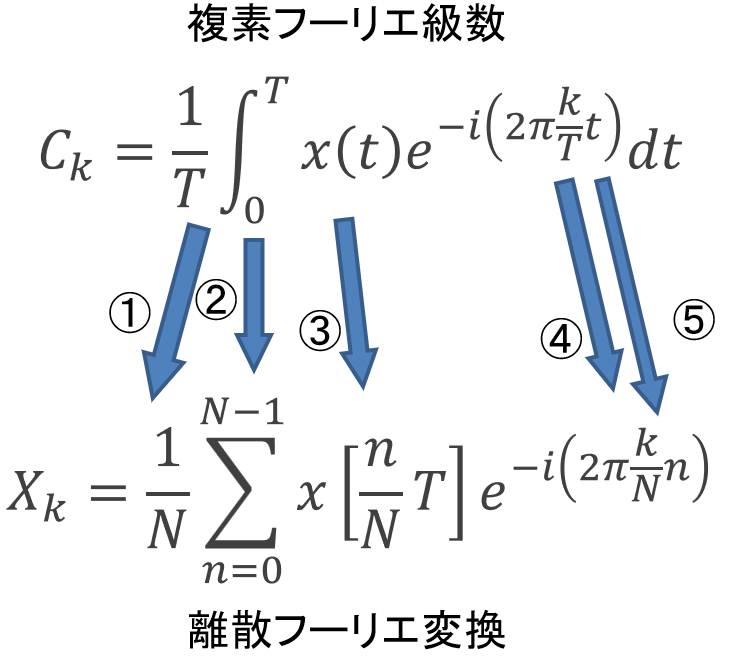
図1：複素フーリエ級数から離散フーリエ変換へ
まず、複素フーリエ級数の周期Tに注目します。連続信号の時は、信号の周期をT[sec]で表していました。これが離散信号になると時間の単位が[sample]に変わります。サンプリング周期は1周期T[sec]をN分割した周期であると定義しているので、1周期の長さはN[sample]に置き換わります（図２①）。
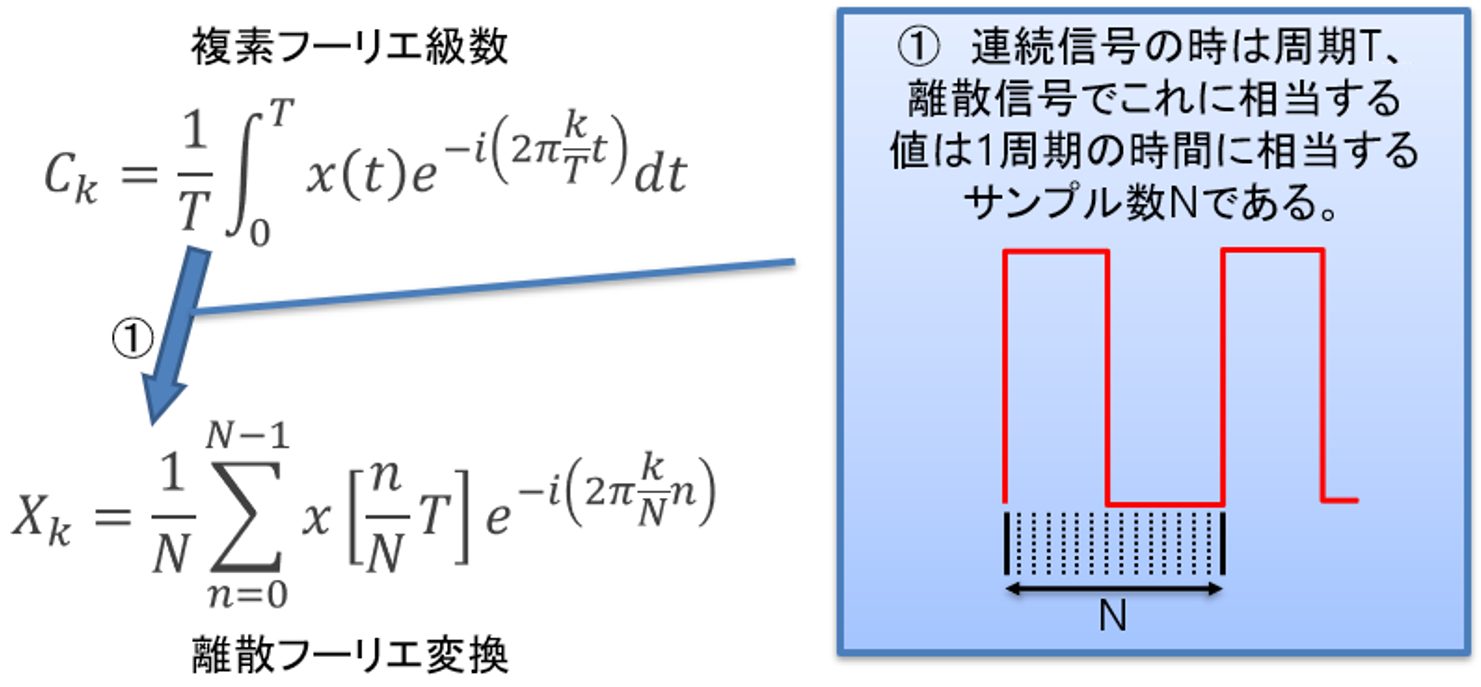
図2：離散フーリエ変換を読み解く（１）
次に積分記号に着目します。積分は連続信号を無限小の区間に区切って積み上げたものでした。ところが前回話した通り、離散信号の世界では「最小の時間単位が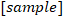
に」なります。従って積み上げる単位は無限小ではなくて具体的な大きさである[sample]単位になります。これはもはや積分ではなくて単なる合計、すなわち総和記号Σで表記できることになります。また積分範囲の上限はTでしたが、総和範囲の上限はN-1になります。連続信号の周期Tが離散信号でNに置き換わるのは、先述の①と同様の考え方です。離散信号列の添字が0から始まるので、その分総和範囲の上限は-1されています（図３②）。
また入力信号xはt（信号の開始から何[sec]経ったかを示す実数）を引数とした連続信号でしたが、これがn（信号の開始から何[sample]目かを示す整数）を引数とした離散信号に置き換わります（図３③）。
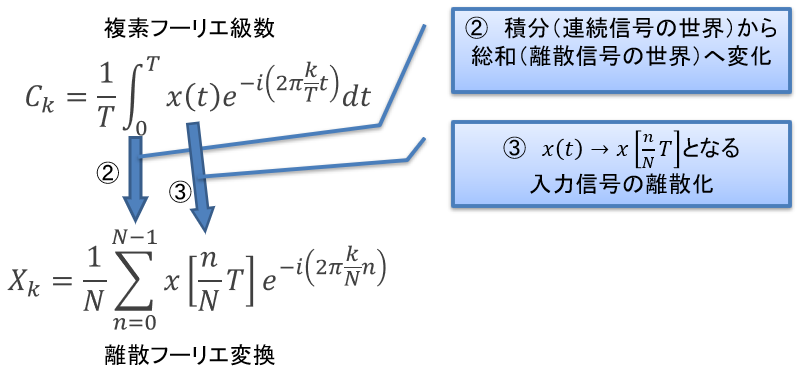
図3：離散フーリエ変換を読み解く（２）
続いて、複素指数関数のカッコ内に着目します。ここも先述の①と同様の考え方で連続信号の周期Tが離散信号でNに置き換わります（図４④）。また先述の③と同様の考え方で連続信号の引数tが、離散信号の引数nに置き換わります（図４⑤）。
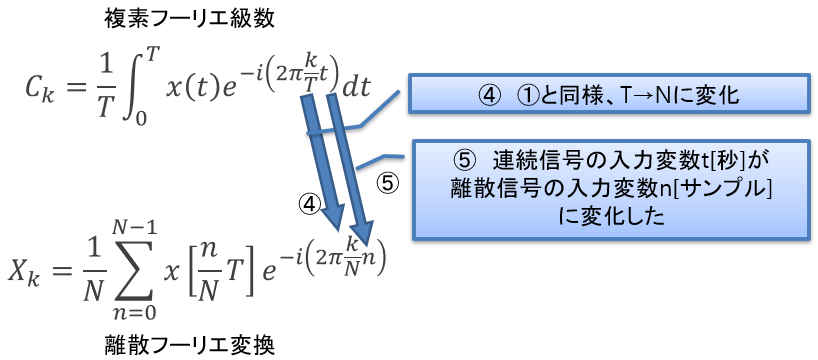
図4：離散フーリエ変換を読み解く（３）
小さな具体例を計算してみる
ごく簡単な具体例を1つ計算してみます。この後のFFT（高速フーリエ変換）につながる議論を理解するためには、ここはぜひ面倒でも手計算でチャレンジして頂きたいと思います。まずは手計算の流れを順に説明していきますので、紙とペンを手元に用意して、順番に書き写して流れを追いかけながら理解して下さい。
例として、以下の連続信号を取り上げます
この信号をT/4秒ごとにサンプリングして、離散信号にします。上式の
tに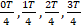
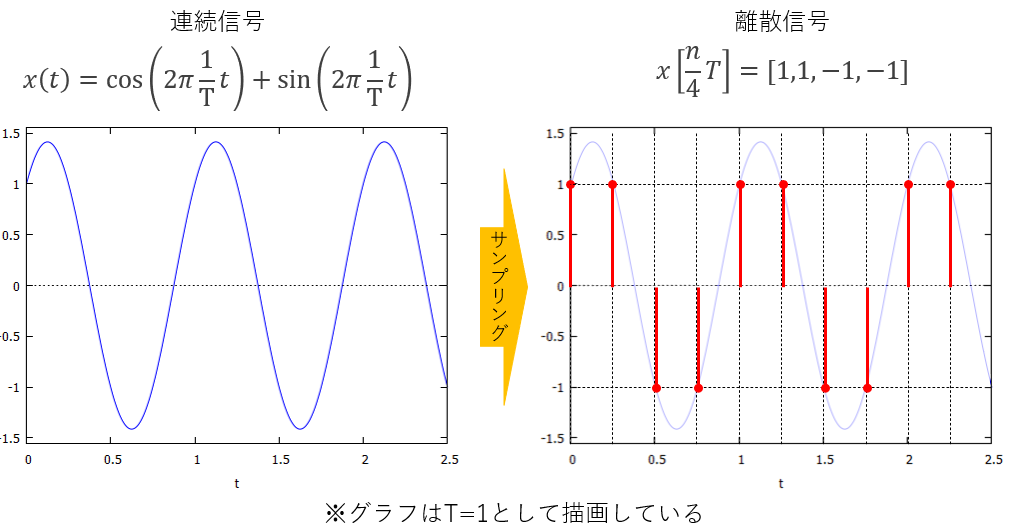
を代入して計算すると、[1, 1, -1, -1]という結果を得ます。これがx(t)の1周期をサンプリングした離散信号になります。
図5：例題信号のサンプリング
この後、行列を使って計算をしていくので、離散信号を列ベクトルの形で書きます。
これを離散フーリエ変換の公式に代入します。分割数Nには4を代入しています。
全ての行に共通している
を行列の外にくくり出します。
各行の総和記号を展開します。
ここで変数nと変数kだったところに注目すると、図6のようにnは横方向・kは縦方向に変化していることがわかります。
図6：n,kの変化
このような時、行列の内積を求める計算を逆に使う事で、2つの行列に分割することができます。
行列の内積（左の行列は横に、右の行列は縦になぞりながら積和する）に沿って計算すると、確かに同じものであることがわかります。1行目だけ計算して確認してみましょう（図７）行列に分解する前の式がちゃんと再現できています。
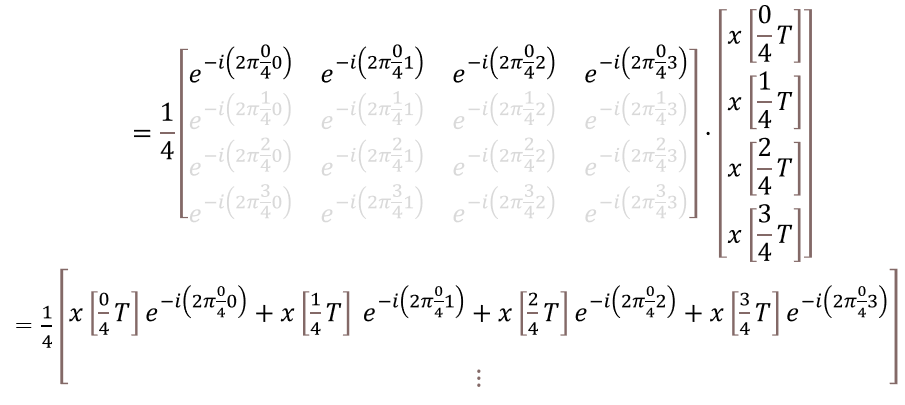
図7：内積を計算してみる
さてここまでの手続きで、離散フーリエ変換が2つの行列の積として表現できることがわかりました。右側の行列は入力離散信号を列ベクトルにしたものそのままです。
左側の行列には複素指数関数が並んでいますが、この行列に変数は含まれておらず、全て具体的な値を求める事ができる行列（定数行列）です。仮にこの行列にRと名前を付けると、以下のように大変きれいな形に表現することができます。
言い換えれば、適切な行列Rを作る方法が見つかれば、入力信号（の列ベクトル）にRを左からかけてあげるだけで離散フーリエ変換は実現できます。またRを計算しやすいように工夫できれば全体の計算が効率化されて処理速度が速くなる（というよりもむしろ、効率化できる場所はそこしかない）こともイメージできるのではないでしょうか。
行列Rの中をさらに計算していきます。まず、カッコの中を一度全て計算してしまいます。
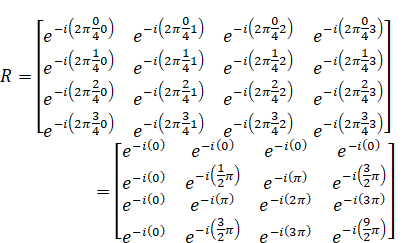
続いて、指数のカッコ外にあるマイナスをカッコの中に入れてしまいます。
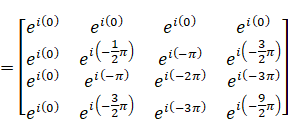
このあと、オイラーの公式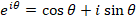
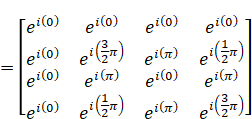
を使って計算を進めていきます。その場合カッコの中は偏角θと考えられるので0～2πの範囲に書き直すことができます。偏角がマイナスであること、つまり角度をx軸から時計回りにとっていることに注意して計算すると次のようになります。
角度の関係を図示すると図８のようになります。
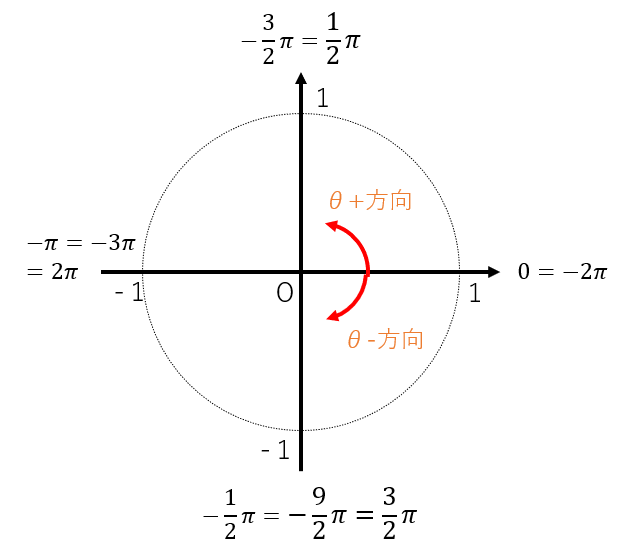
図8：行列Rの各成分が持つ偏角
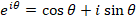
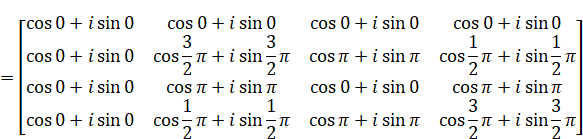
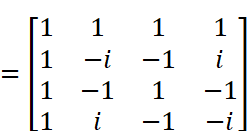
オイラーの公式を使って各成分を計算します。
これで行列Rが具体的に求められたので、離散フーリエ変換を実行できます。
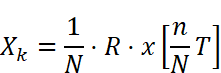
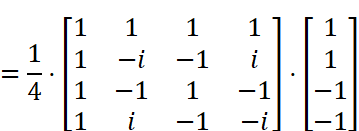
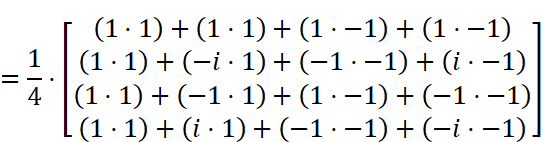
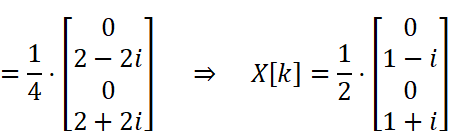
これで離散フーリエ変換が完了しました！これはフーリエ変換でいうスペクトル関数を求めた状態に相当します。実用的にはここから振幅スペクトル・位相スペクトル・パワースペクトルを求めて使用することがほとんどですので、さらにもうひと踏ん張りして各種スペクトルを求めてみましょう。
計算で求めたX[k]は複素数の値であり、複素数の絶対値を求めると振幅スペクトルになります。また複素数の偏角を求めると位相スペクトルになります。
0の絶対値は0で自明です。(1-i)の絶対値を求めるために複素平面を考えましょう（図９）。
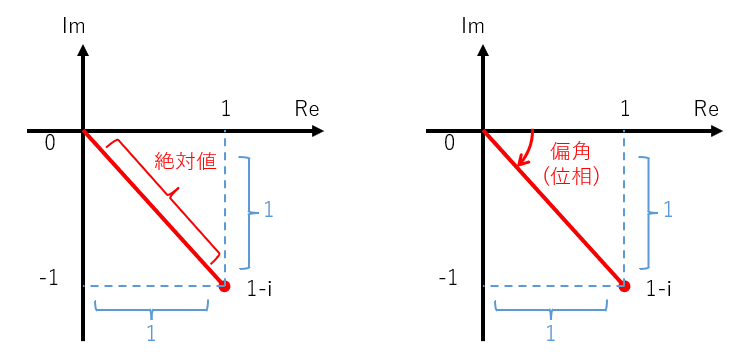
図9：(1-i)の絶対値と偏角
横軸（実軸）が1、縦軸（虚軸）が-1の点が(1-i)を表す点になります。複素数の絶対値はこの点と原点との直線距離に相当するので、三平方の定理を使用して
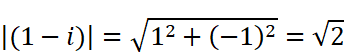
と求められます。また偏角は横軸（実軸）から測った角度ですので、
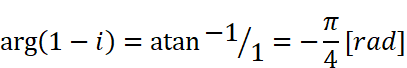
と求められます。atanはアークタンジェント、つまりtan（タンジェント）の逆関数です。(1+i)も同様に
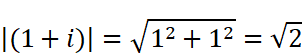
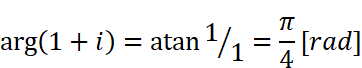
と求められます。
従って振幅スペクトルは次のようになります。
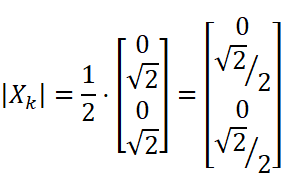
位相スペクトルは次のようになります。複素数に定数(1/2)をかけても偏角は変化しないため計算から消えていることに注意して下さい。
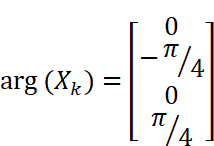
パワースペクトルは振幅スペクトルの2乗になります。
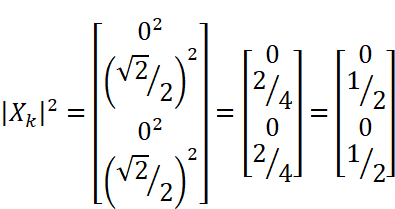
以上のスペクトルをグラフ化すると図１０のようになります。
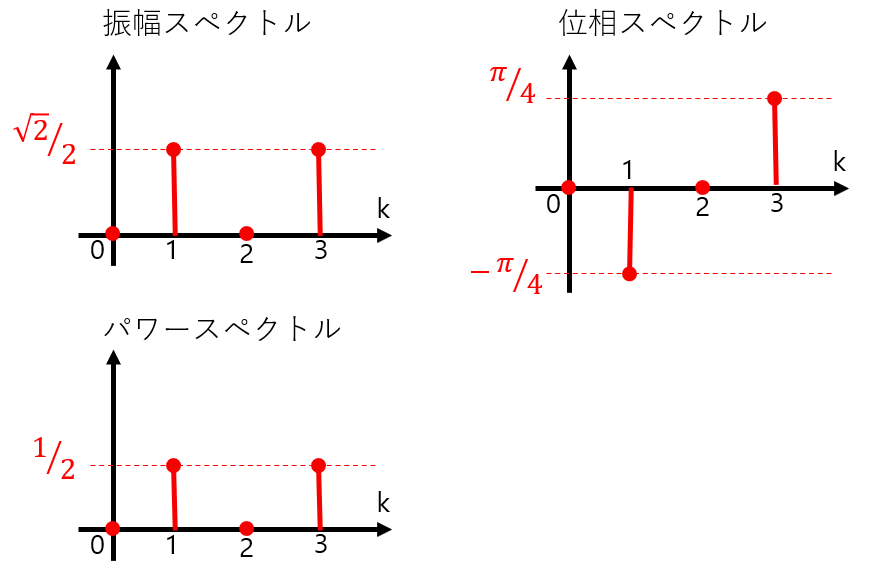
図10：例題信号の各スペクトル
次回は、同じ信号のサンプリング周期を半分にした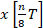
を離散フーリエ変換しながら、行列Rの性質を考えていきたいと思います。
こちらも是非
“もっと見る” ブログ
はじめての耐量子暗号
量子コンピューティングはさまざまな面で明るい未来のために期待される技術である反面、その演算能力をセキュリティ上の攻撃に使われることを考えると、既存の暗号技術にとって深刻な脅威でもあります。
Arm®対応のWindows IoT OS 【Windows IoT on Arm】を評価ボードで動かしてみる
組み込み機器向けOS、Windows 10/11 IoT Enterprise(以下Windows IoT)がサポートするArmプラットフォームが拡大しています。Windows IoT on Armは、Windows IoTのメリットそのまま、より低コストで低消費電力というArmならではのメリットもございます
センサーのすべてがわかる！組み込み技術者のための基礎知識
私たちの生活を豊かにするために欠かせないセンサー。そんなセンサーの仕組みや種類について、分かりやすく解説していきます。