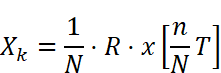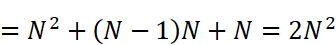離散フーリエ変換の計算量
いよいよ本連載の大きな目標である離散フーリエ変換（FFT）の手前までやってきました。
前回までの記事で、離散フーリエ変換（DFT）のコアとなる部分は回転因子行列Rと入力信号ベクトルxの積であること、具体的には
という式である事を説明してきました。
ところで、コンピュータプログラムの世界には「計算量」という概念があります。ある入力データを元にプログラム処理を実行するとき、実行開始から完了までにどれだけの時間が必要になるか、を表す値です。
4点DFTの場合、回転因子行列Rと入力信号ベクトルxの（行列の）積を求めるためには、16回のラスター（数値）積と12回の和が必要です。その後で各成分（4点）に1/Nをかける必要があるので、全体で20回の積と12回の和が必要になります。積と和では処理に必要な時間が違いますが、ざっくり1つの「演算」という単位として考えれば、4点DFTには20+12＝32回の演算が必要という事です。8点DFTの場合も同様に考えると72回の積と56回の和を求めることになり、合計で128回の演算が必要になります。
さらに一般化してN点DFTの場合にはどうなるかというと、演算回数は
となります。Nは入力データの数を表していて、《入力データ数の2乗》に比例した演算回数が必要であることがわかります。このような処理を、「計算量が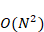
の処理である」といいます（ランダウのO記法という表現方法です）。入力データが大きくなると指数的に演算回数が増えてしまうため、この処理は「遅い」部類の処理です。実用的な音の分析としては512点とか1024点でフーリエ変換を行う事もよくあるので、それぞれ約52万回・210万回の演算が必要になってしまいます。
では「速い」処理はどのような処理でしょうか。どこからが「速い」と言えるのか明確な基準があるわけではありませんが、O記法で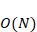
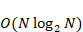
（《入力データ数》に比例する演算回数）や
（《入力データ数と入力データ数の2を底とした対数の積》に比例する演算量）の処理だと「速い」と評価されます。
この後学んでいく高速フーリエ変換は、離散フーリエ変換と同じ計算結果を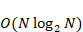の計算量で求める事ができます。
これがどれほどありがたい事かを示すため、DFTとFFTの処理に必要なおおよその演算回数をグラフにすると図1のようになります。Nが大きくなるほどFFTの速さが際立っています。1024点で計算をするときであれば、FFTの演算回数はDFTのわずか2%で済んでしまいます。
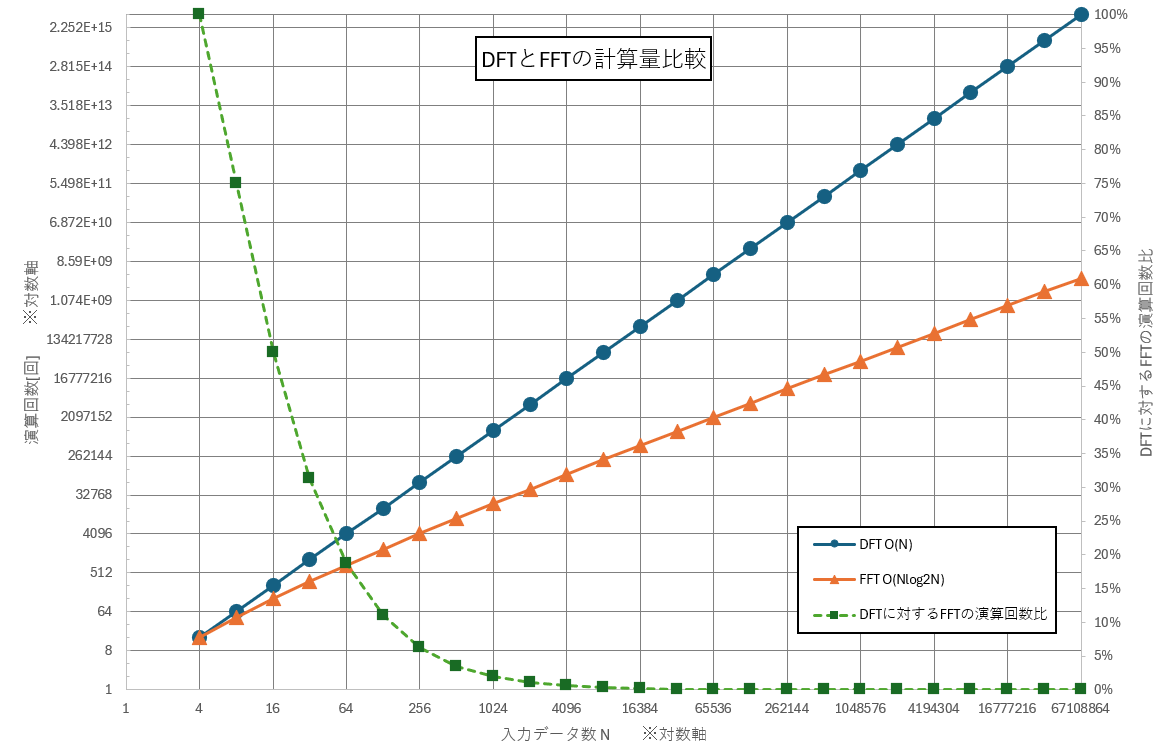
図1：DFTとFFTの計算量比較
コンピュータの性能はそのままで処理速度を速くするためには「そもそものデータ数を減らす」「不要な処理をなくす」「同じ計算を何度もしないように工夫する」などの方法が使えます。DFTの場合、入力データ（N）を減らせば処理時間は確かに早くなりますが、同時に分析結果が荒くなってしまう（周波数分解能が悪くなる）という副作用があり、嬉しくありません。そして行列の積を求めるために必要な演算しかしていないので、一見「不要な処理」は見当たりません。
そこで、回転因子がまさに「回転」している事に着目します。回転因子行列を作っている回転因子は、それぞれが「複素平面状の単位円をN等分したどこかの点」を示していました。円を一周すれば元の位置に戻ってくるので、「1周以上回転した点」は「1周未満回転した点」と必ず重なっています。つまり、単純に行列の積を用いてDFTを行う際に大量に出現する「1周以上回転した点」の計算は「1周未満回転した点」と重複しているのです。
アメリカの数学者クーリー(James William Cooley)とテューキー(John Wilder Tukey)の両名は、この回転因子行列の計算から無駄をなくし、速く、効率よく計算するアルゴリズムを発見しました。この手法が現在高速フーリエ変換（FFT）と呼ばれているものになります。
ちょっと余談：テューキーの功績
テューキーは、2進数の1ケタを表すビット（bit）という言葉を生み出した人でもあります。1940年代中ごろに”Binary Digit”を短縮して”bit”という造語を産み出しました。その後1948年にクロード・シャノンが発表した「通信の数学的理論」という論文で、2進数の1ケタと「情報量」の概念が結び付けられました。そこでbitが情報量の単位となり、世界中で広く使われるようになりました。
FFTを導き出す
クーリーとテューキーが示した手法には「時間間引きFFT」と「周波数間引きFFT」がありますが、ここでは「時間間引きFFT」を紹介します。
8点DFT(N=8)の回転因子行列Rから始めます。省略記法を使ってＲを書くと次のようになります。
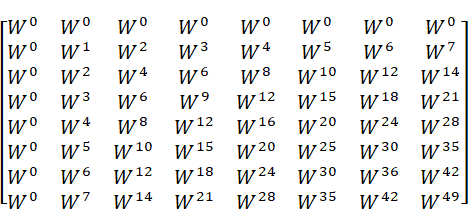
8点DFTなので、独立した成分は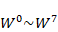
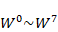
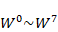
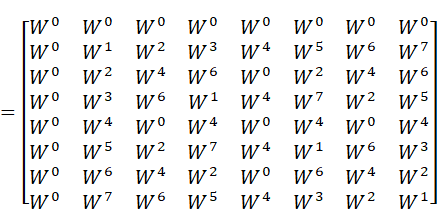
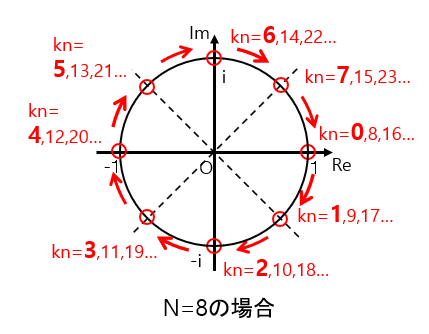
までです。それ以外はのどれかの点と同一なので（図2参照）、全ての成分をの範囲に収めます。
図2：回転因子の図解（N＝8）
得られた行列を、左右で半分に分け、さらに偶数行と奇数行で比較します。赤枠青枠・実線点線で区別したものが図3です。
図3：回転行列を左右列・偶奇行で分割
偶数行（0,2,4,6：青色）にだけ着目すると、左と右で同じ値が並んでいることがわかります（図4）。
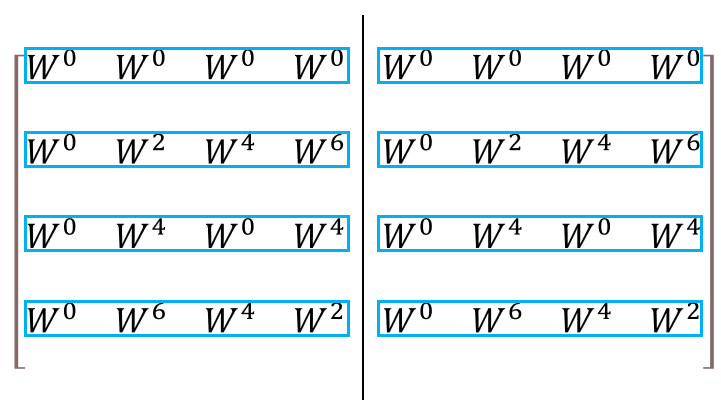
図4：偶数行だけ取り出した回転行列
奇数行（1,3,5,7：赤色）だけに着目すると、左半分（実線枠）と右半分（点線枠）は一見異なります（図5）。
図5：奇数行だけ取り出した回転行列
左右をよく見比べてみると、右側（点線枠）は左側（実線枠）の動きをちょうど半円（180°）ずらしたもの（半周期ずらしたものと表現しても良い）になっています。例として2行目と8行目を図示したものが図6です。
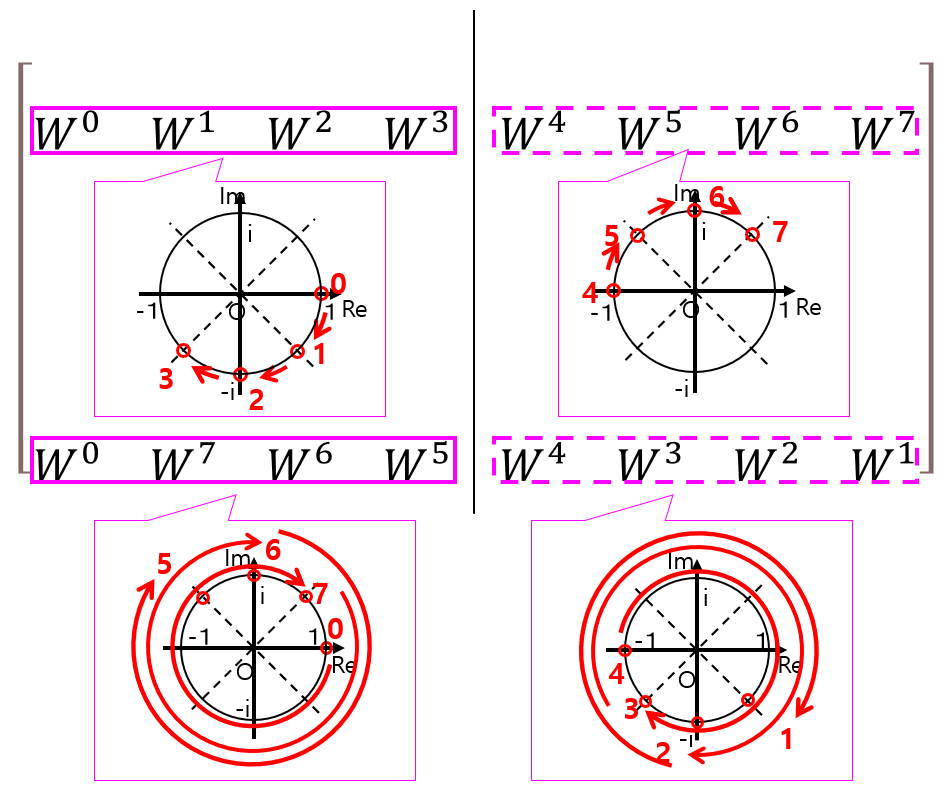
図6：回転行列奇数行の左右を比較
偶数行と奇数行それぞれに特徴があるので、偶数行と奇数行を分離します。また、「右半分」の計算を「左半分」の計算と同時に行うように工夫します。言葉では説明が難しいので図7を見て下さい。
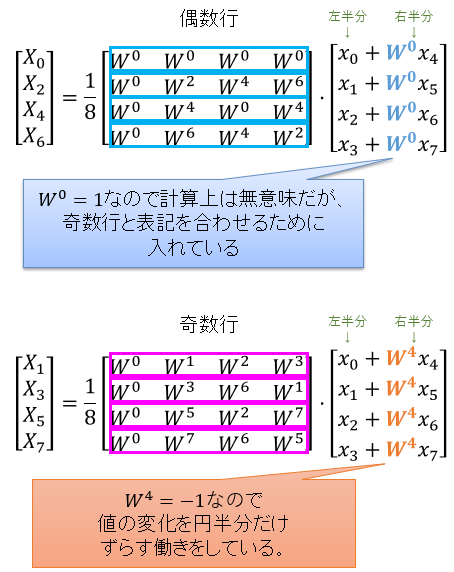
図7：回転行列の左右をまとめてしまう
これで、もともと8×8だった回転因子行列を、4×4の回転因子行列2つ（偶数行に由来するもの、奇数行に由来するもの）に分割することができました。つまり、8点DFTは２つの4点DFTに分割できることになります。同様の考え方で、さらに4×4の行列を2×2の行列2つに分割することができ、最終的には4つの2点DFTに分割されます。
分割するためには「回転因子行列を左右に分割する」「左と右を比べて、同じ《周期ズレ》を持つ行を抽出して固める」という処理を繰り返し行います。8点DFTの回転因子行列が4つの行列に分割されるまで、残りの計算手順と結果を図8及び図9に示します。
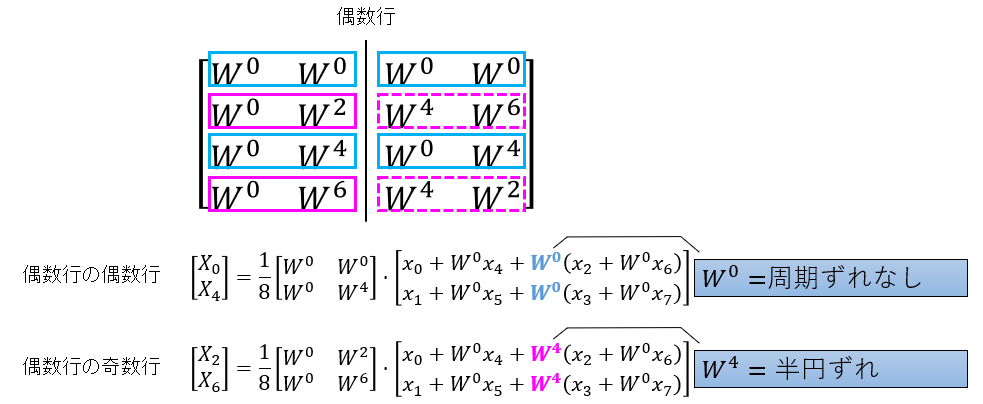
図8：元々偶数行だった4×4回転因子行列を、さらに2×2回転因子行列に分割する
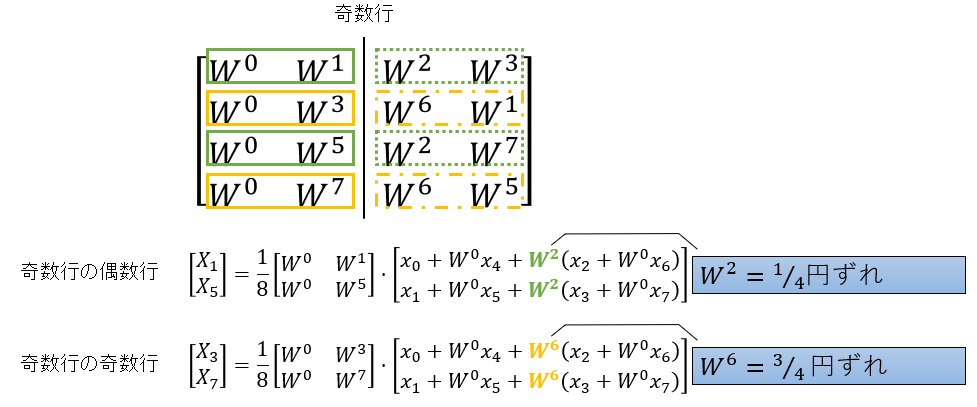
図9：元々奇数行だった4×4回転因子行列を、さらに2×2回転因子行列に分割する
今回は8点DFTを出発点として回転因子行列を2×2まで分割しましたが、N点DFTのNが2のべき乗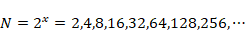
であれば、同様の考え方で回転因子行列を2×2まで分割することが可能であり、これによってDFTの計算に含まれる無駄を排除して高速に計算を行うことが可能になります。
試しに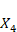
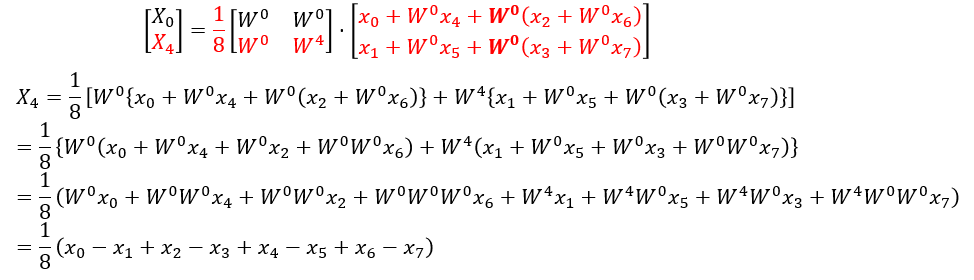
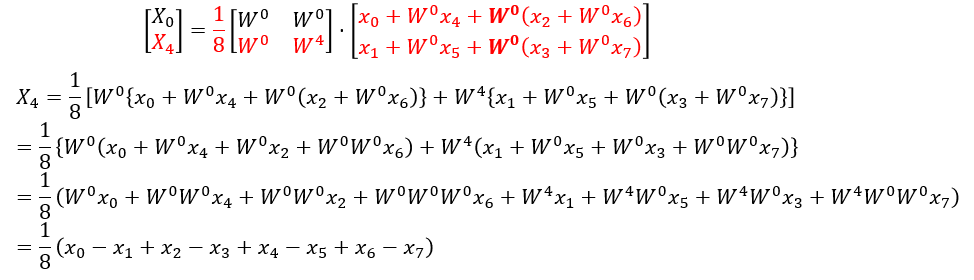
を求める計算をしてみます。図8内「偶数行の偶数行」から、該当部分だけ計算すると図10になります。
図10：分割後の式（FFT）からX4の値を求めてみる
元々の8点DFTの公式から該当部分を抜き出して計算してみると図11のようになります。
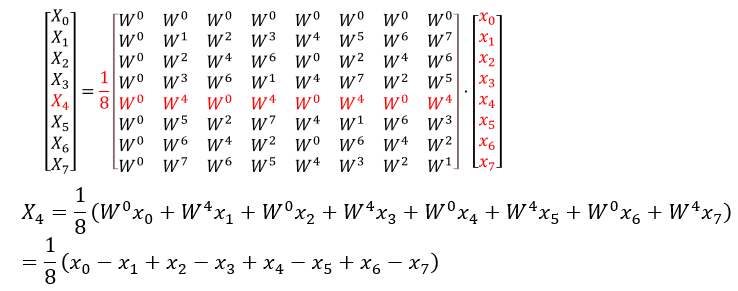
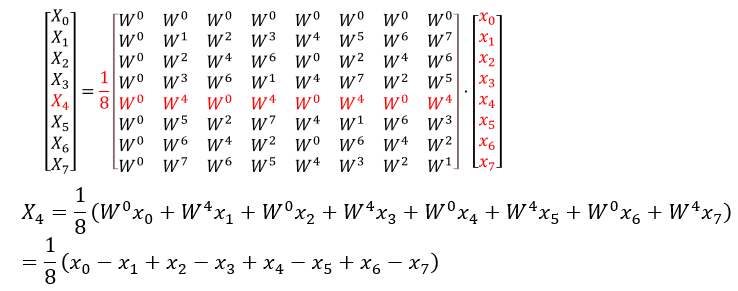
図11：分割前の式（DFT）からX4を求めてみる
図10の結果と図11の結果は一致しており、FFTとDFTで同じ結果が得られている事が確認できました。
次回は、このFFTの中に潜む「蝶(Butterfly)」の話をします。
こちらも是非
“もっと見る” ブログ
はじめての耐量子暗号
量子コンピューティングはさまざまな面で明るい未来のために期待される技術である反面、その演算能力をセキュリティ上の攻撃に使われることを考えると、既存の暗号技術にとって深刻な脅威でもあります。
Arm®対応のWindows IoT OS 【Windows IoT on Arm】を評価ボードで動かしてみる
組み込み機器向けOS、Windows 10/11 IoT Enterprise(以下Windows IoT)がサポートするArmプラットフォームが拡大しています。Windows IoT on Armは、Windows IoTのメリットそのまま、より低コストで低消費電力というArmならではのメリットもございます
【フーリエ変換から離散フーリエ変換へ：フーリエ変換編3】イメージでしっかりつかむ信号処理〜基礎から学ぶFFT〜
「フーリエ級数展開」「フーリエ変換」は連続信号を対象としているので、そのままではコンピュータで使うことができません。コンピュータで周波数分析を行うためには、離散信号に対応したフーリエ変換を考える必要があります。