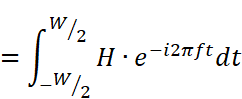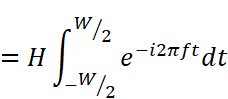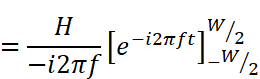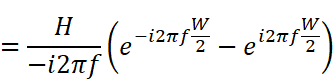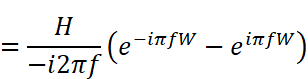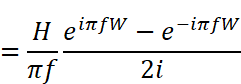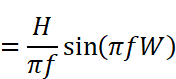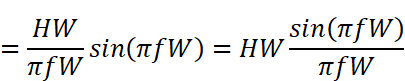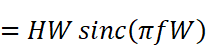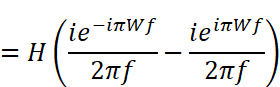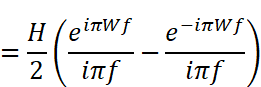実際にフーリエ変換をしてみよう
単発パルス（方形パルス）のフーリエ変換
前回はフーリエ変換の意味と、複素フーリエ係数を求める式からフーリエ変換の式が得られる事を説明しました。今回は実践編という事でフーリエ変換を試してみたいと思います。
図1に示すような、時刻t=0に中心がある単発パルス（方形パルス）のフーリエ変換を行ってみましょう。パルスの横幅をW、パルスの高さ（振幅）をHと定義しています。
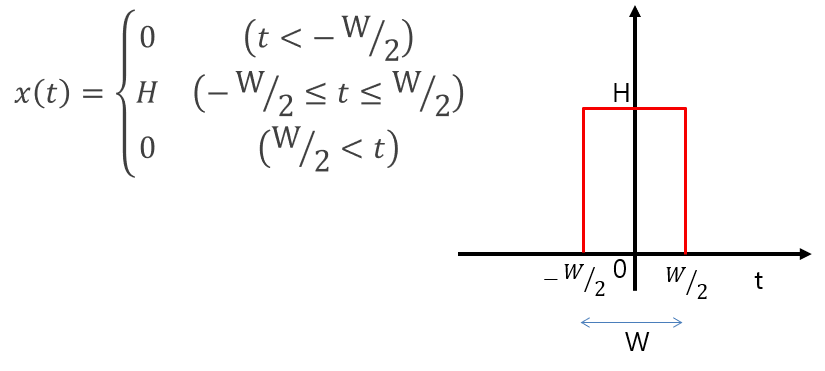
図1：単発パルス（方形パルス）の定義
本連載ではできるだけ面倒な手計算をしないという方針ですが、この例題に関しては手計算を示したいので、ちょっと辛抱してお付き合いください。
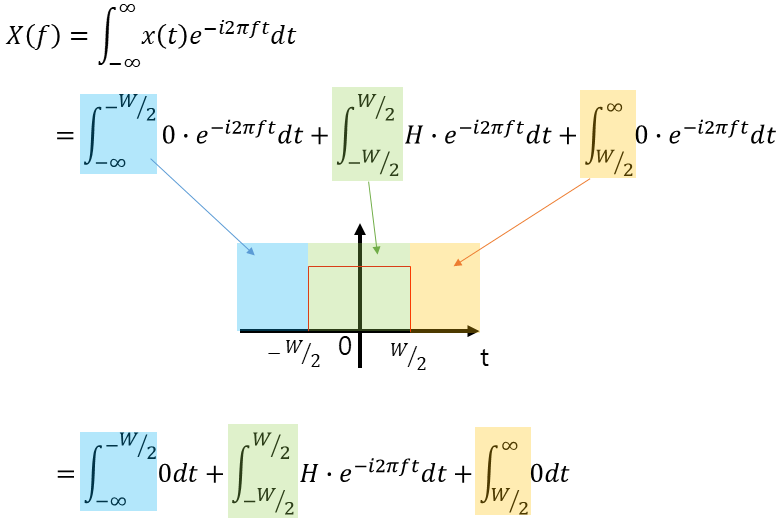
このx(t)をフーリエ変換の公式に代入します。パルス波形がある所とない所（マイナス側・プラス側）の3つに積分区間が分割できます。図1に示したx(t)の定義と積分区間の関係性をよくチェックして下さい。
0をいくら積分しても0であることは自明なので、真ん中の第2項だけが有効な計算です。
Hは時間に関係ない定数なので、積分の外にくくり出すことができます。
積分の中に指数関数だけが残りました。この先の計算をするためには、本連載では説明していない「置換積分」というテクニックが必要になるのですが、とりあえず結果だけ示すと
となります。
右側のカッコ内は2つの複素指数の引き算なのですが、ここを見て「複素形式の三角関数に形が似ている」と気づけた人は大変センスの良い人です！少々トリッキーな事をして、分母の-2iだけをカッコの中に移すと次のように整理することができます。マイナスが移動した結果、分子の引き算順序が逆転している事に注意して下さい。
複素形式の三角関数では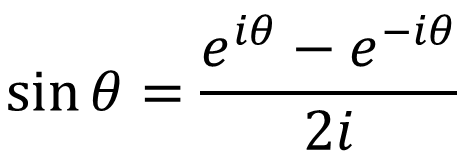
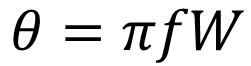
と定義されているので、
と解釈すると
という、大変すっきりした形に整います。
さらにここからもう一工夫することができまして、左側の分数に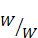
をかけ算して（これは約分すると1なので、かけ算しても値は変化しません）分母を右のsin関数へうつします。
右側の分数は、分子にsin関数、分母に（分子の）sin関数の中身が置かれています。これにはsinc関数（シンクまたはジンク関数と読む）という特別な名前がついており、
と、大変きれいにまとまります。
Wolfram AlphaおよびMaximaで計算してみましょう。パルスの大きさHとパルスの幅Wを文字のまま計算したものと、具体例としてH=5,W=0.5を代入したものを計算してみます。
まずはWolfram Alphaで文字のまま計算させてみます。
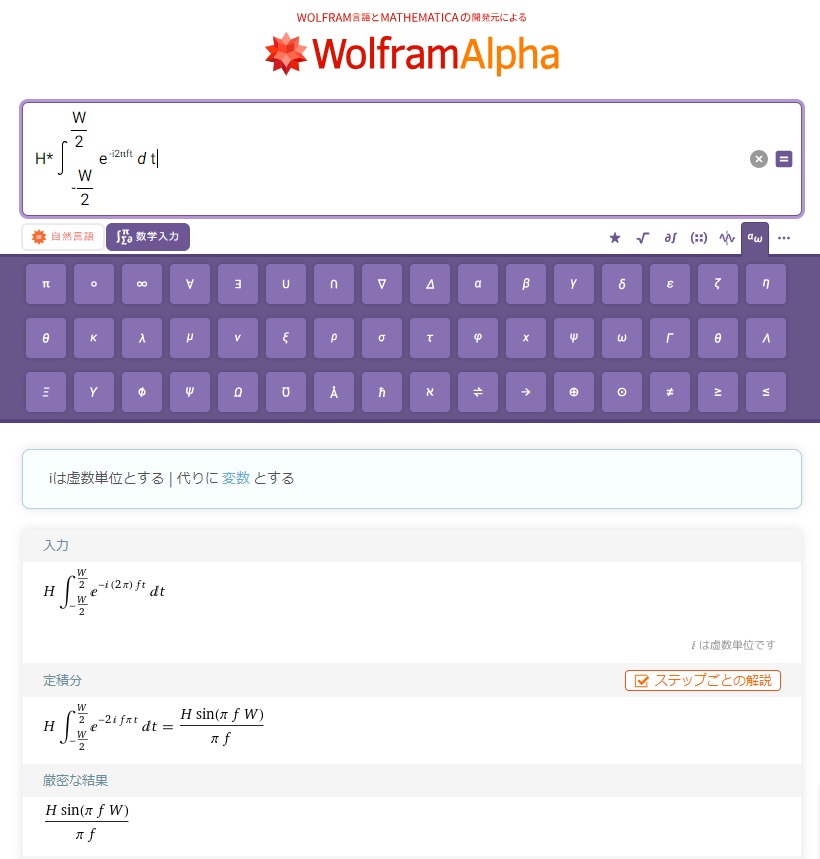
図2：単発パルスのフーリエ変換（Wolfram Alpha）
Sinc関数まではまとまりませんでしたが、正しく計算できています。続いて値を代入した状態で計算させてみます。
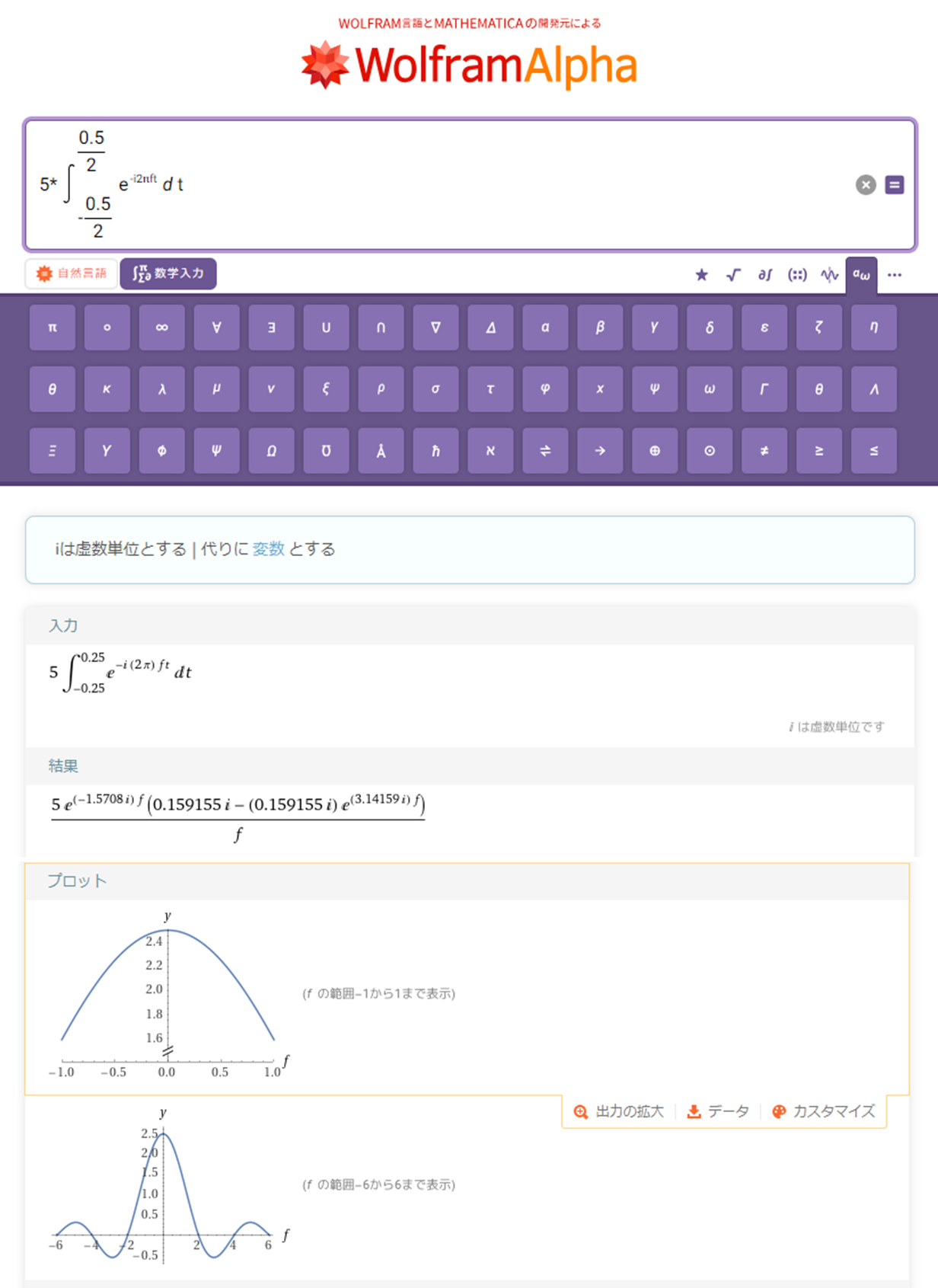
図3：単発パルスのフーリエ変換：具体例（Wolfram Alpha）
プロット結果を見ると、中心から離れるに従って徐々にsin関数の振幅が小さくなっていることが読み取れます。これがsinc関数の形状です。
続いてMaximaを使って文字のまま計算させてみましょう。
図4：単発パルスのフーリエ変換（Maxima）
一見今までと異なる計算結果が出ているように見えますが、よく見るとこの式は以下のように整理できます。つまり複素形式のsin関数で表現されているだけで、等価な値です。
続いて値を代入した状態で計算とプロットをさせてみます。
図5：単発パルスのフーリエ変換：具体例（Maxima）
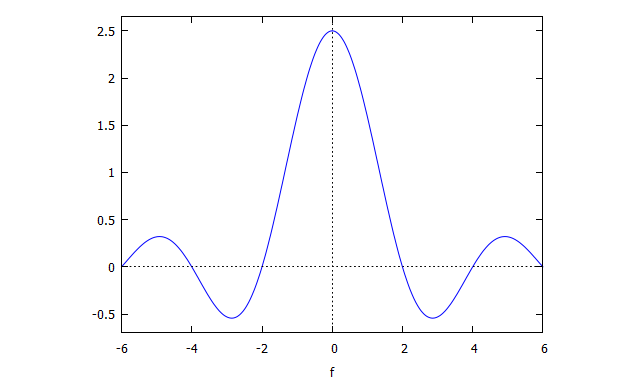
図6：単発パルスのフーリエ変換：具体例プロット結果（Maxima）
複素形式のsin関数になっていますが、Wolfram Alphaと同じ波形がプロットされました。Maximaではプロット範囲を自由に変えられるので、もっと広い範囲（-12≦f≦12）をプロットしてみましょう。
図7：単発パルスのフーリエ変換：具体例（２）（Maxima）
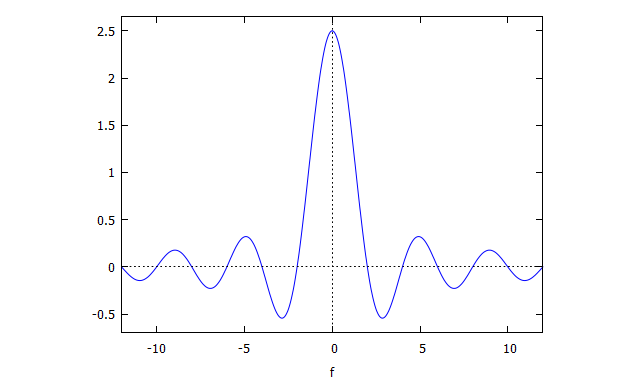
図8：単発パルスのフーリエ変換：具体例（２）プロット結果（Maxima）
単発パルス（方形パルス）のスペクトル
続いて、今計算した単発パルス（方形パルス）のスペクトルを求めてみましょう。
まずWolfram Alphaで求めてみます。振幅スペクトルはフーリエ変換結果（スペクトル関数）の絶対値（abs）を求める事で得られます。絶対値なので、振幅が負だった部分が正方向に折り返されます。
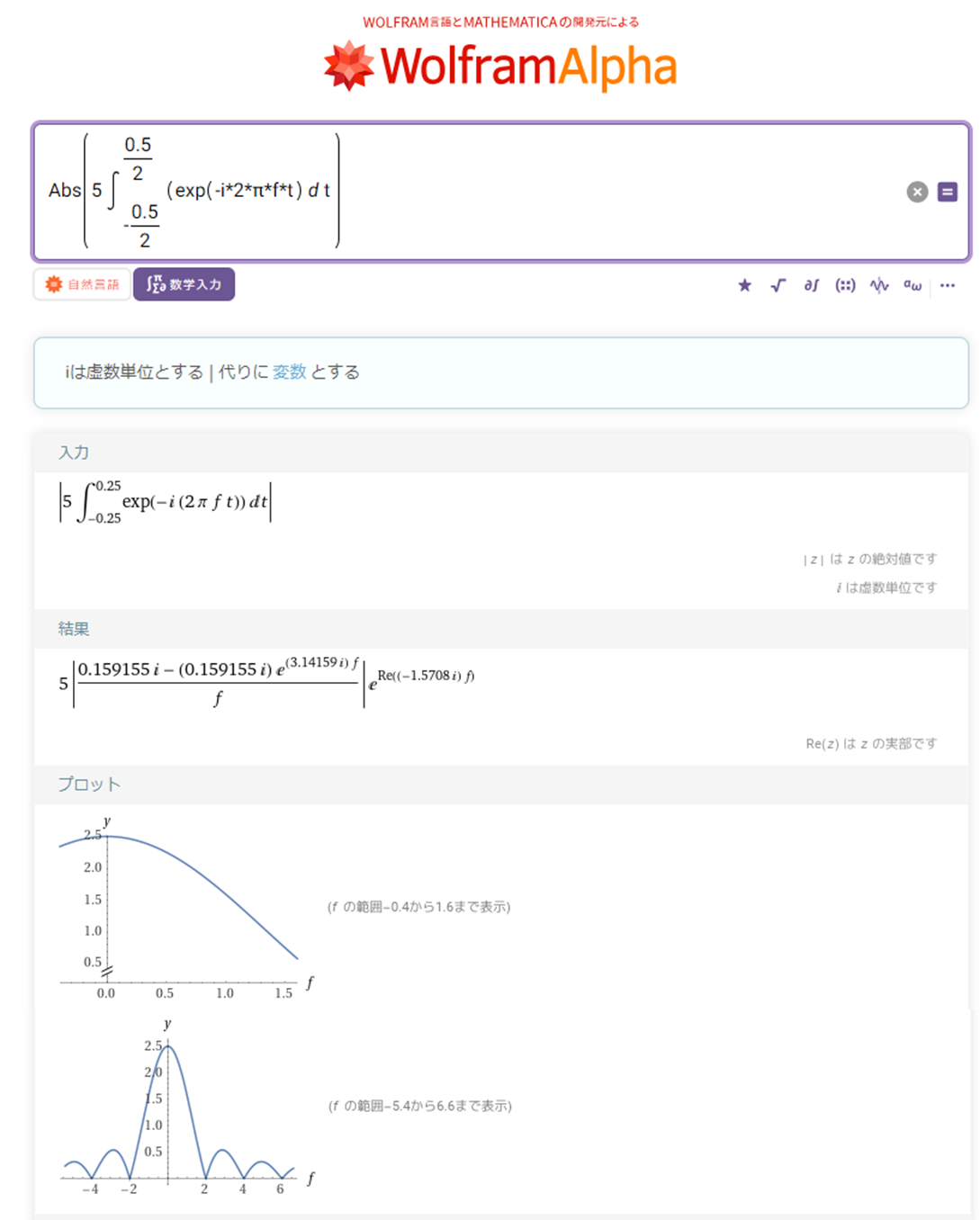
図9：振幅スペクトル（Wolfram Alpha）
位相スペクトルはAbs（絶対値）関数を、位相を求めるArg関数に置き換えれば求められます（ただし残念ながら無料版のWolfram Alphaでは上手くプロットされませんでした）
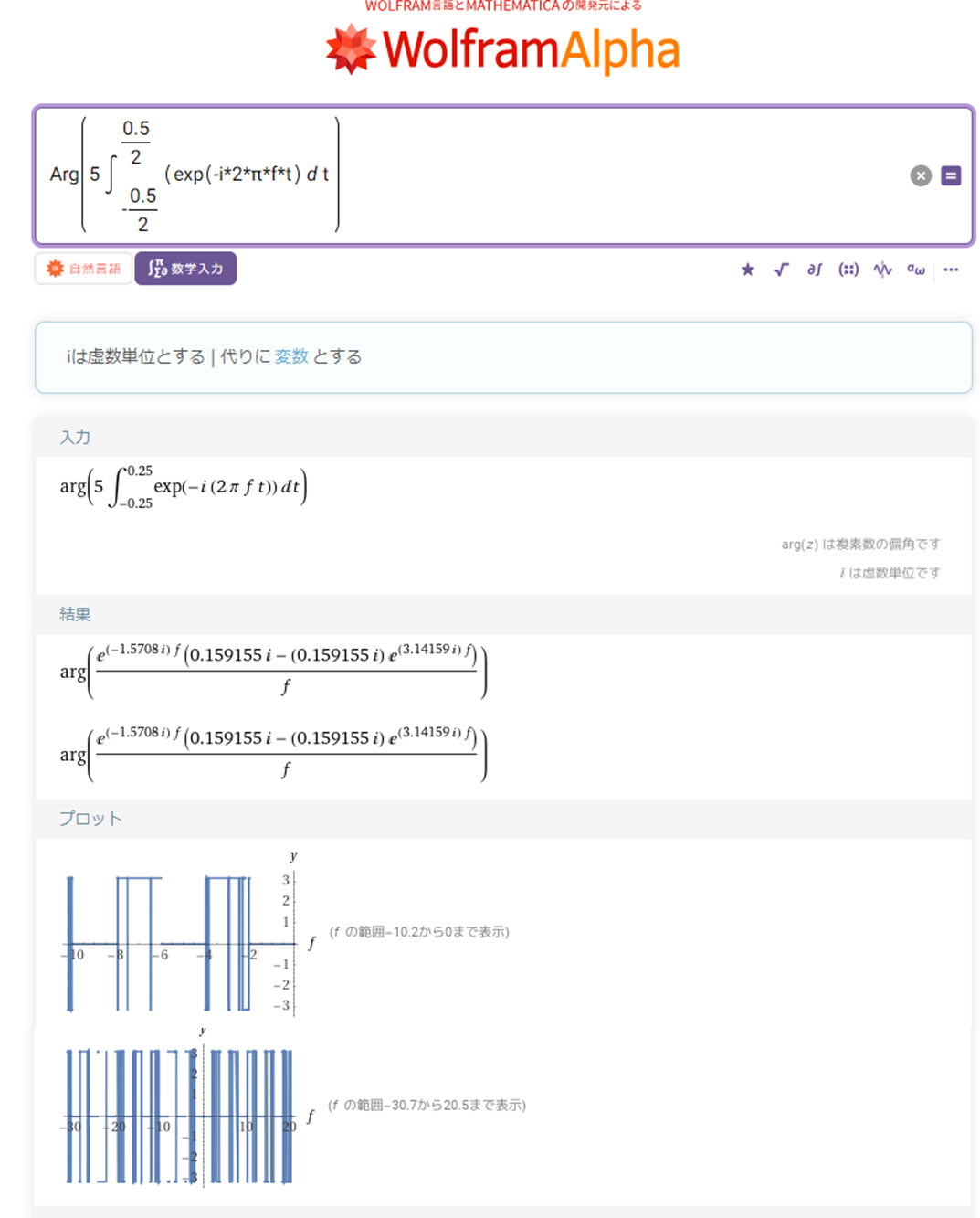
図10：位相スペクトル（Wolfram Alpha）
パワースペクトルは振幅スペクトルを2乗して求められます。
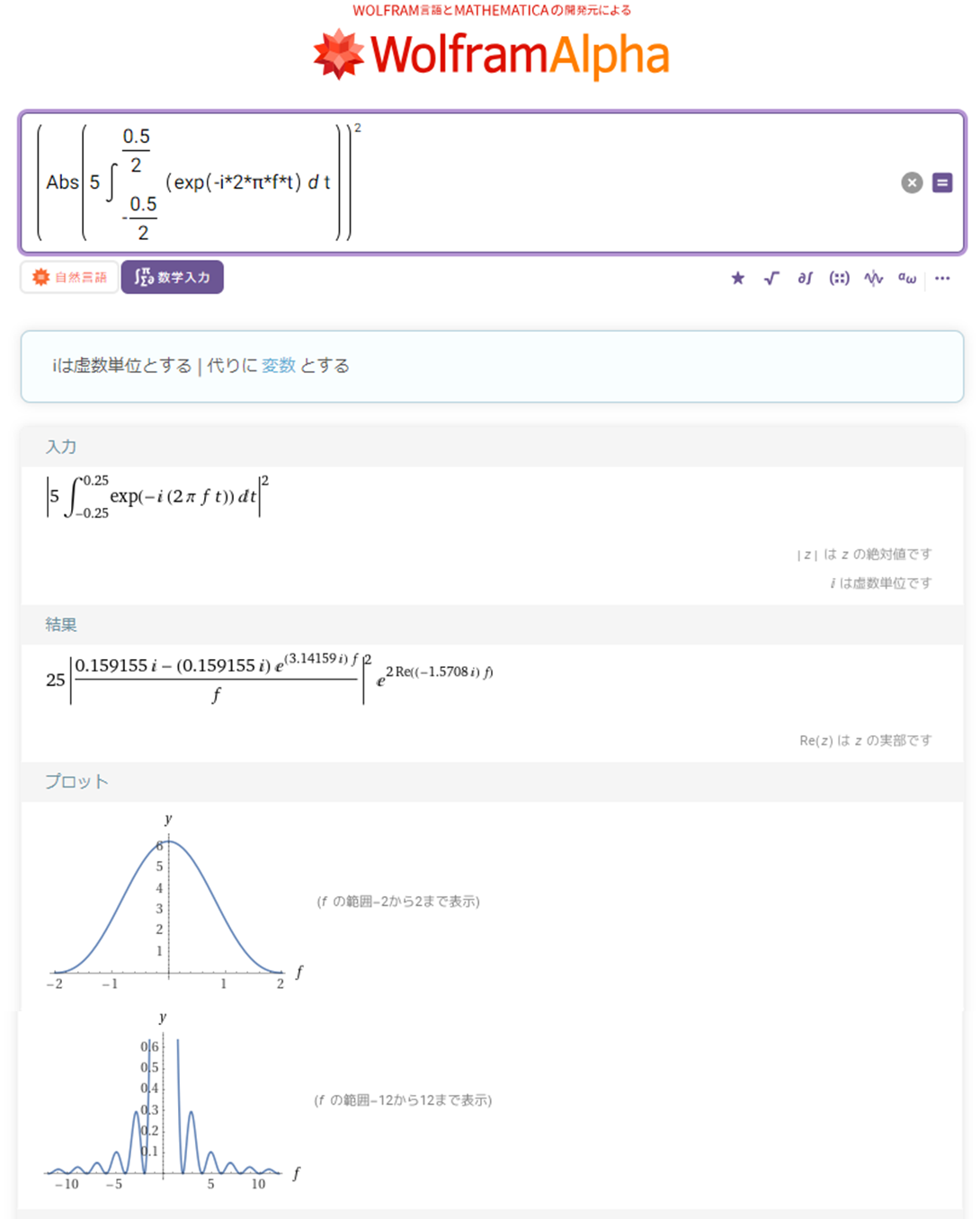
図11：パワースペクトル（Wolfram Alpha）
同じことをMaximaでも行ってみましょう。振幅スペクトルはWolfram Alphaと同様にabs関数で求められます。
図12：振幅スペクトル（Maxima）
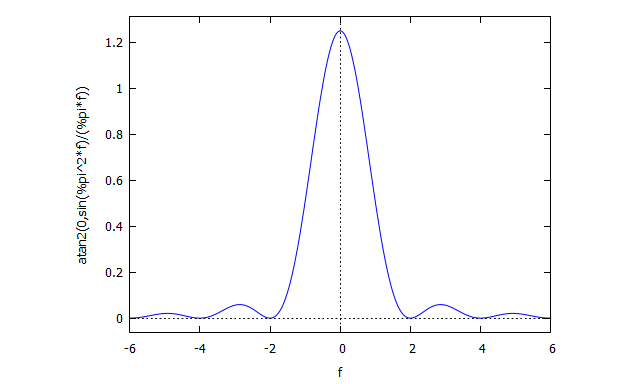
図13：振幅スペクトルプロット（Maxima）
位相スペクトルはcarg関数で求めます（Wolfram Alphaと関数名が異なるので注意して下さい）
図14：位相スペクトル（Maxima）
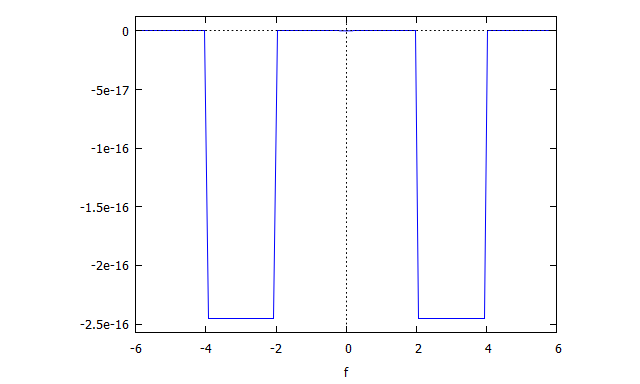
図15：位相スペクトルプロット（Maxima）
パワースペクトルは振幅スペクトルを2乗して求められます。
図16：パワースペクトル（Maxima）
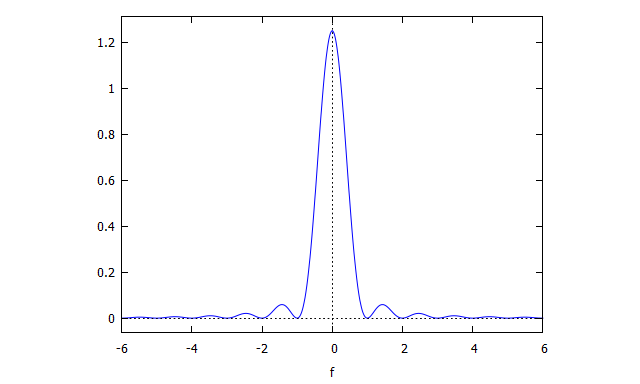
図17：パワースペクトルプロット（Maxima）
今回は計算が多くて大変だったかもしれません。お疲れ様でした。
次回は「フーリエ変換」を「離散フーリエ変換」に進化させる過程をお話しします。
こちらも是非
“もっと見る” ブログ
はじめてのセキュア転送〜組み込み向けMCUでセキュア転送を動かしてみる〜
セキュアファイル転送の基本機能について説明します。また、理解を助けるために実際のMCUでセキュアファイル転送を行う簡単なサンプルプログラムを動かしてみたいと思います。
【離散フーリエ変換を実現してくれる行列：フーリエ変換編5】イメージでしっかりつかむ信号処理〜基礎から学ぶFFT〜
離散フーリエ変換の対象となっている離散入力信号が8個あるので、これに対する離散フーリエ変換を「8点の離散フーリエ変換」とか、さらに短縮して「8点DFT」と言ったりします。同様に前回の例題は4点DFTといいます。
【離散フーリエ変換を読み解く：フーリエ変換編4】イメージでしっかりつかむ信号処理〜基礎から学ぶFFT〜
複雑に見えますが、離散フーリエ変換の式と複素フーリエ級数の式（係数を求める式）とを照らし合わせると、複素フーリエ級数を自然な形で離散信号用に書き換えたものであることがわかります。図１のように両者を並べて、5つのポイント（①～⑤）に注目しながら照らし合わせてみましょう。