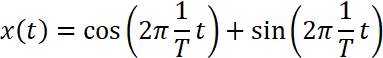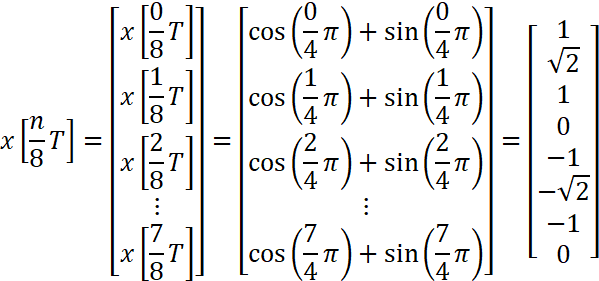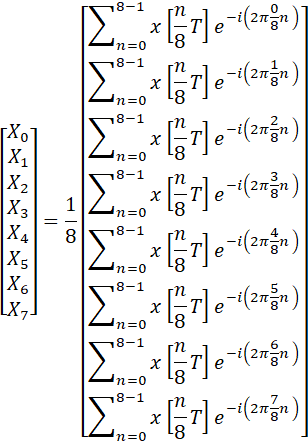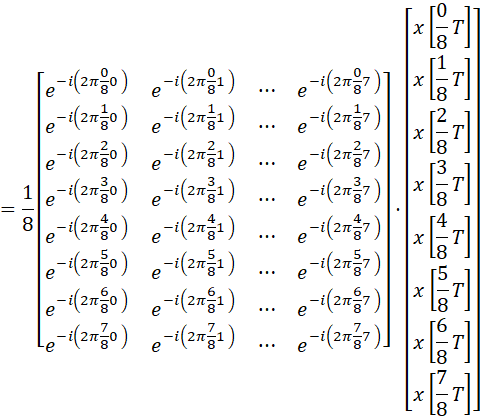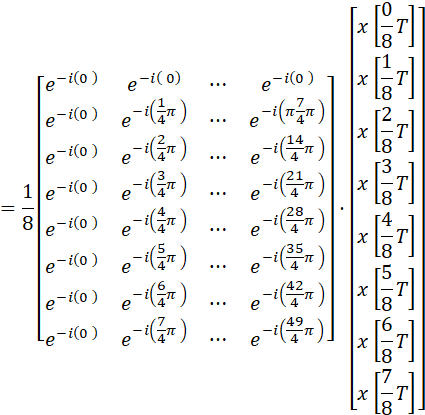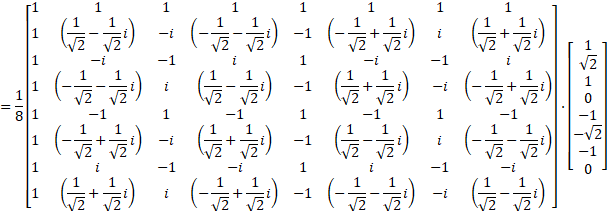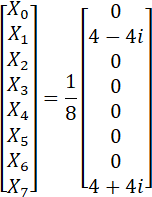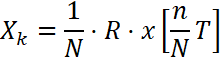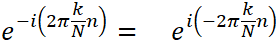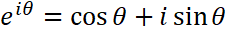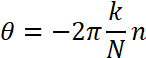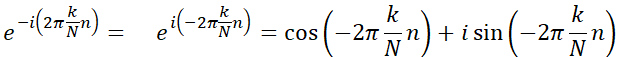8点離散フーリエ変換にトライする
前回の例題で使用した連続信号
を今度はT/8秒ごとにサンプリングして、離散信号にします。tに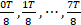
を代入して計算します。今後の計算のために列ベクトルの形で書いておきます。
図示すると図１のようになります。
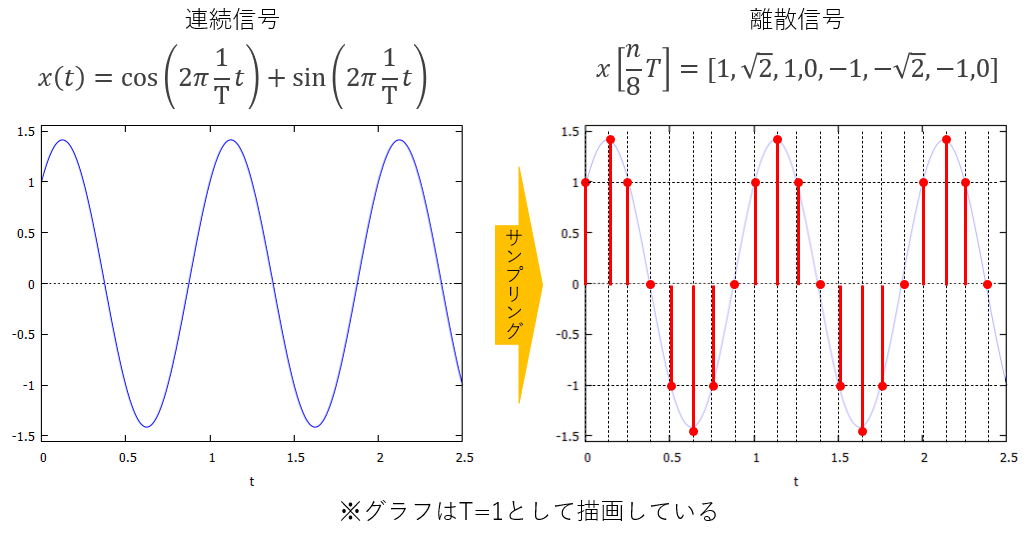
図1：例題信号のサンプリング
離散フーリエ変換の対象となっている離散入力信号が8個あるので、これに対する離散フーリエ変換を「8点の離散フーリエ変換」とか、さらに短縮して「8点DFT」と言ったりします。同様に前回の例題は4点DFTといいます。
これを離散フーリエ変換の公式にいれて、まずはそのまま計算をしてみます。
行列を2つに分け、定数行列Rと入力信号ベクトルの積にします。
カッコの中を計算します
オイラーの公式を使って展開します。
行列のかけ算をすると次のようになります。
ここから各スペクトルを求めると図２のようになります。4点DFTの時とほぼ同じようなスペクトルが得られます。
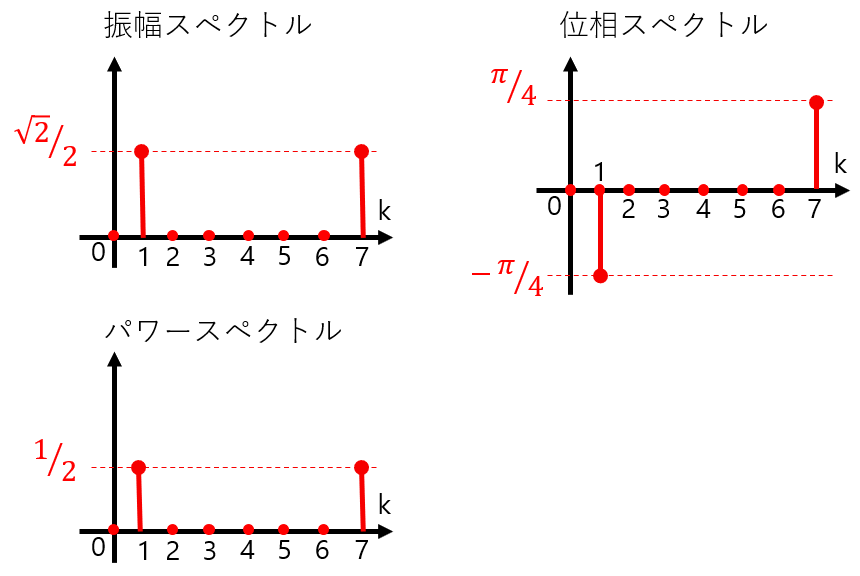
図2：例題信号の各スペクトル（8点DFT）
定数行列Rの意味を考える
前回説明したように、そして先ほどの8点DFTでも見たように、DFTは定数行列Rをうまく作ってあげれば
という単純なスカラーと行列のかけ算の形で表現することができます。この定数行列Rの意味を紐解いていくと、何点のDFTでもすぐに行うことができるようになりますし、本連載の大きな到達目標である高速フーリエ変換（FFT）にもつながっていきます。
まず、8点DFTの定数行列Rを省略せずにもう一度図３に示します。横方向に0…7と変化している部分と縦方向に0…7と変化している部分があることを再度確認してください。
図3：行列Rの完全版
定数行列Rの各成分は
という形をしています。オイラーの公式
の左辺と比べると
と考えることができるので、行列Rの各成分は
となります。
このθは複素数の角度（偏角）を表しています。わかりやすくするためθの式をすこし変形したものを図４に示します。変数k,nは必ず正整数であることに注意が必要です。
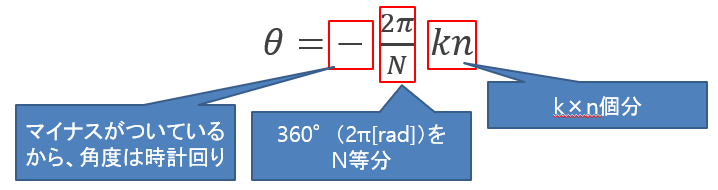
図4：偏角θの読み解き
そしてcosは単位円上にある点のx座標、sinは単位円上にある点のy座標として定義された事を加味すると、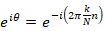
は「複素平面上の単位円をＮ分割した点」を表します。
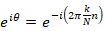
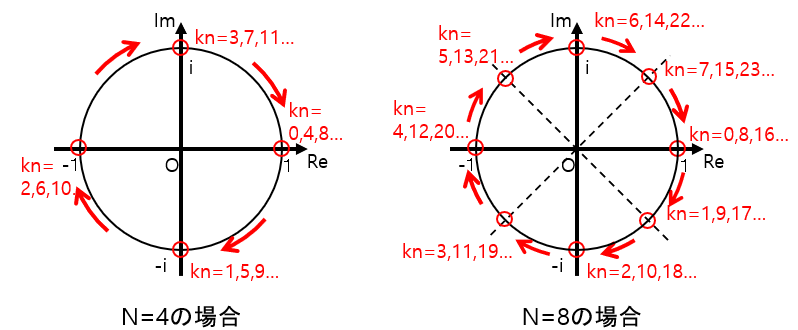
kn=0の場所(1+0i＝単位円と横軸(実軸)の交点)を起点とし、knが1増えるたびに円を2π/N[rad]だけ時計回りに進んだ位置を示します。は単位円をぐるぐる回る点を表しているため「回転因子」と呼ばれます。また回転因子が集まった行列Rを「回転因子行列」と呼びます（図5）。
図5：回転因子のふるまい
これ以降、回転因子を簡単に書くための省略記法を導入します。（複素平面上の）単位円が横軸（主軸）と交わる点を起点として、単位円をN分割した点を時計回りに数え、M番目の点を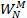
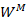
と書くことにします。ただし分割数Nが明らかな場合はさらに省略して
と表記します。
省略記法を使って8点DFT(N=8)の回転因子行列Rを書くと次のようになります。
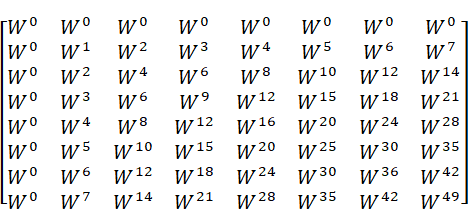
回転因子行列Rには規則性があります。まず大きさはN行N列であり、回転因子の指数は1行目・1列目が0固定です。2行目は左から1ずつ指数が増え、3行目は左から2ずつ指数が増え…N行目は左から(N-1)ずつ指数が増えます（図6）。
図6：回転因子行列の規則性
図6で示しているのはN=8の例ですが、その他のNでも同様です（Nは2以上の正整数です。後述するFFTで使用する都合上、通常は2のべき乗（2,4,8,16,32…）を使用します）。
これを「回転」という観点で図示すると図7のようになります。
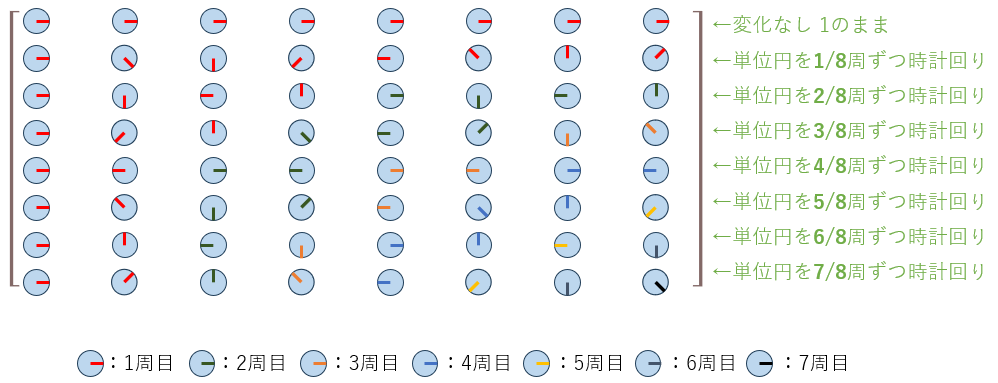
図7：回転因子行列の図示
各行を、左から右に向かって時間が進むと考えると、下に行くほど「速い回転」を表していることがご理解いただけるでしょうか。より正確に言うならば、1行下に行くにつれて回転の角速度が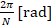
ずつ速くなっています。
同様に4点DFT（N=4）の回転因子行列を表すと図8のようになります。
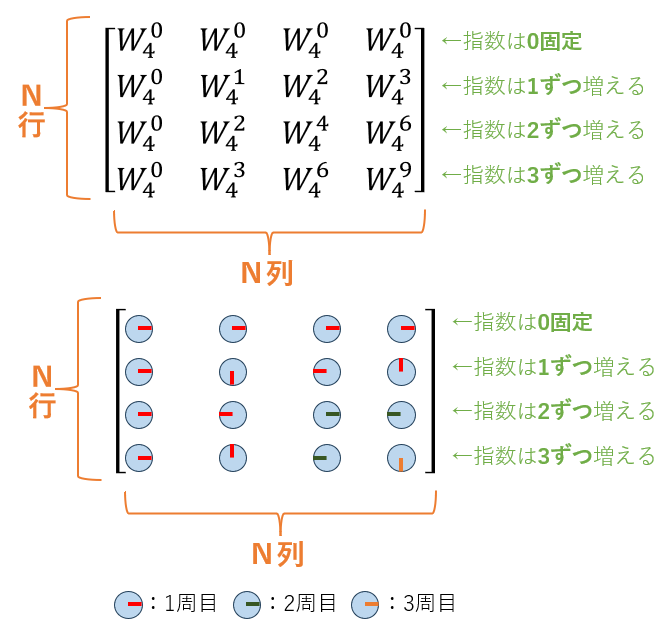
図8：4点DFTの回転因子行列
回転因子Wの指数が持っている規則性を理解すると、あとは16点DFTでも32点DFTでも512点DFTでも・・・機械的に回転因子行列を作ることができるようになります。
次回は、DFTで求めたスペクトルの読み方について詳しく説明します。
こちらも是非
“もっと見る” ブログ
はじめての耐量子暗号
量子コンピューティングはさまざまな面で明るい未来のために期待される技術である反面、その演算能力をセキュリティ上の攻撃に使われることを考えると、既存の暗号技術にとって深刻な脅威でもあります。
Arm®対応のWindows IoT OS 【Windows IoT on Arm】を評価ボードで動かしてみる
組み込み機器向けOS、Windows 10/11 IoT Enterprise(以下Windows IoT)がサポートするArmプラットフォームが拡大しています。Windows IoT on Armは、Windows IoTのメリットそのまま、より低コストで低消費電力というArmならではのメリットもございます
【フーリエ級数からフーリエ変換へ：フーリエ変換編1】イメージでしっかりつかむ信号処理〜基礎から学ぶFFT〜
ここまで学んできたフーリエ級数展開は、「入力信号が周期波形でなければならない」という制約がありました。上図のような太鼓の音、すなわち単発波形は、フーリエ級数展開できないのでしょうか