高校から消えてしまった「行列」
ある年代より上の人たちには驚きかもしれませんが、かつて高校数学で学んでいた「行列」は、現在高等学校の学習指導要領から消えていました（厳密に言えば消えたというのは言い過ぎで、、2009年公示、2013年度高校入学生より実施の学習指導要領から行列は大幅に内容を縮小して「数学活用」という科目に移っていました。しかし実体としては「数学活用」を設置した学校は少なかったようです）。2018年告示、2022年度高校入学生から実施されている現行の学習指導要領では、（新カリキュラムの）数学Cにて行列を扱うようになったため、従来（2012年以前）ほどの分量ではないにせよ、部分的に復活しました。
図1：高等学校学習指導要領で「行列」を扱う科目
理工系の大学ではほぼ必ずと言っていいほど必要になる知識ですので、高校で学習していなくても大学に入ってから学習するのですが、文系の大学に進んだ方では「行列」を全く学んだことがない、という方もいるかもしれません（ちなみに筆者は2001年高校入学ですが、工業高校だったために数学Cが選択科目になっていて未履修でした。その後大学に入ってから苦労して学びました）。そのような方でもついてこられるように、最低限知っていて欲しい行列の知識を、丁寧に説明していきたいと思います。
あくまでも最小限の説明しかしませんので、これ以上学びたい人は大学で使用する「線形代数学」の入門書などを探してみるとよいでしょう。
行列・ベクトルとは
「いくつかの値を縦横に並べて、長方形状にしたもの」を「行列」といいます（逆に、行列ではない、単独の値を「スカラー」といいます）。行列を作るそれぞれの値の事を「成分」や「行列要素」といいます。横方向の並びを「行(Row)」、縦方向の並びを「列(Col)」といいます。行・列の成分数が同じ場合、その行列を「正方行列」といいます。
行列を記号で表す時は通常大文字のアルファベット1文字で表現し、イタリック体または太字を用います。行列の内容を示すときは通常、要素の並びを大きな丸かっこまたは角かっこで囲います。行列を構成する各要素を記号で表現する時は、行列の記号を小文字にして、右下に行番号・列番号を付けます。
図2：行列の表し方
行列のうち、値が一列に並んでいるものを「ベクトル」といいます。特に、値が横一列に並んでいるものを「行ベクトル」、縦一列に並んでいるものを「列ベクトル」といいます。ベクトルであることを強調して記号を付ける場合は、アルファベットの小文字を太字にする場合が多いようです。
図3：ベクトルの表し方
ちょっと余談：ベクトルと矢印
物理学、特に高校などで学ぶ力学の世界では「ベクトル」というと「矢印」のイメージと結びつけ、「向きと量がある」などと考えることが多いです。しかし「ベクトル＝矢印」という理解は誤りです。物理学における「矢印」を表すために、数学の「ベクトル」というツールが便利だから使用しているというだけです。
例えば日付を表す年／月／日という時間の組み合わせは（物理的な動きや位置を表す）矢印とは何の関係もありませんが、（2023 01 03）のように並べれば、数学的にはれっきとしたベクトルになります。
行列の和（足し算）と差（引き算）
行列の演算は常に答えが定義されているわけではない事に注意して下さい。行列の和と差は、計算対象となる2つの行列が同じ大きさである時に限って存在します。
計算方法は簡単で、左右の対応する成分を足したり引いたりするだけです。
図4：行列の和と差
具体例を使って、行列の足し算と引き算をやってみましょう。P,Eという3行3列の行列を使い、和と差を求めてみます。
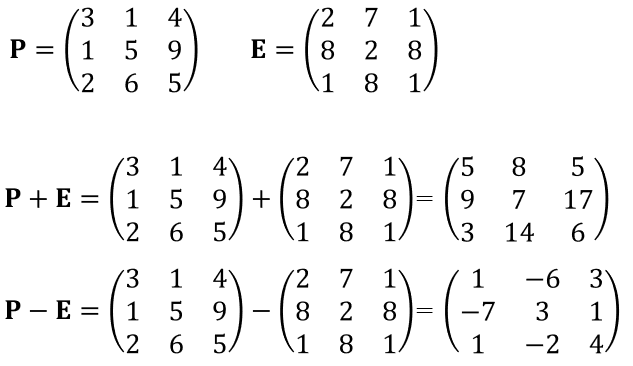
図5：行列の和と差 例題
足し引きしても値が変わらない行列…零行列
全ての要素が0である行列は、足しても引いても答えが変わらない事はすぐにわかるかと思います。すなわち、数字の「０」に相当する行列です。このような行列の事を「零（ゼロ）行列」といい、通常記号Oで表します。
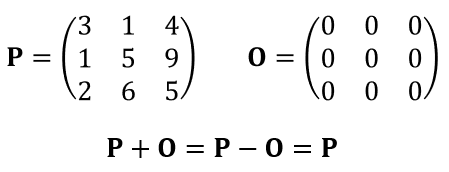
図6：零行列の定義
行列のかけ算
行列の和と差は単純なので、すぐに覚えられると思いますが、少しやっかいなのがかけ算です。行列のかけ算とひとくちに言っても、様々な方法がありますので、これらを整理して理解する必要があります。
行列に対するかけ算は、スカラーをかけるか、行列同士をかけるかの2通りがあります。前者を「スカラー倍」といい、後者は単純に「行列の積」といいます。本稿ではこの後、この「スカラー倍」と「行列の積」についてのみ説明します。
1行だけ、または1列だけの行列を「ベクトル」ということは先に説明しましたが、ベクトル同士のかけ算は、行列の積とはまた別に「内積（スカラー積）」「外積（ベクトル積」の2つが定義されています。「スカラー積」と「スカラー倍」は言葉が似ていますが、全く異なる内容ですので注意して下さい。
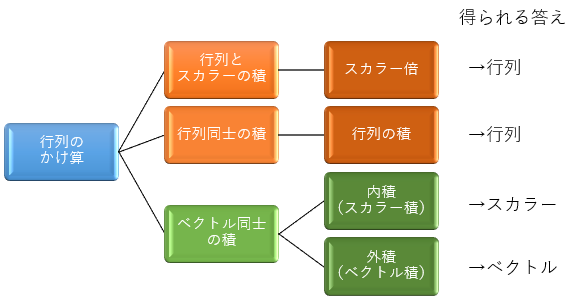
図7：行列のかけ算
行列のスカラー倍（定数倍）
行列とスカラーの積を「スカラー倍」といいます。スカラー倍の計算方法は単純で、行列のすべての要素に対してスカラーをかけ算するだけで求めることができます。
図8：行列のスカラー倍（定数倍）
具体例を使って計算してみましょう。行列Pにスカラー8をかける例です。
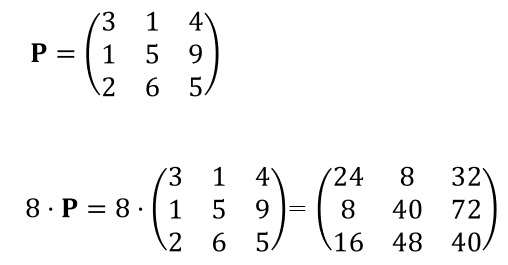
図9：行列の定数倍（スカラー倍） 例題
行列の積
行列同士の積を求める方法はすこしややこしいです。
まずA・Bという計算をするとき、「行列Aの横成分」の数と、「行列Bの縦成分」の数が一致している必要があります。この条件を満たしていないと、そもそも行列の積を求める事ができません（条件を満たさない場合は「答えが存在しない」）。
大切な特徴として、行列の積は「非可換（ひかかん）」という特徴があります。スカラー同士の積であれば、積（かけ算）の順序は入れ替えても問題ありませんでしたが、行列の場合には一般的に積の順序を入れ替えると答えが変わってしまう（あるいは答えが求まらなくなってしまう）ため、自由に順序を入れ替える事が出来ません。このような特性を「非可換（ひかかん）」といいます。（常に非可換というわけではなく、特殊な条件を満たしている時は可換になることもあります）
積の求め方ですが「行・列」という漢字をフックにして覚えるのがわかりやすいでしょう。図の【覚え方】とその下にある計算例を見比べてみて下さい。どのような規則性で計算しているか、わかるでしょうか。
図10：行列の積
図の計算例では、〈2行〉3列の行列Aと3行〈2列〉の行列Bをかけ算しています。〈〉で囲んだ行数・列数が一致しているので、この計算には答えが存在します。得られる答えは〈2行〉〈2列〉の行列が結果として出力されます。
左上の要素に注目しましょう。左上の要素は、「行列Aの1行目を左から右になぞって拾った成分」と「行列Bの1列目を上から下になぞって拾った成分」の積和（それぞれの要素をかけ算して全て合計したもの）になっています。
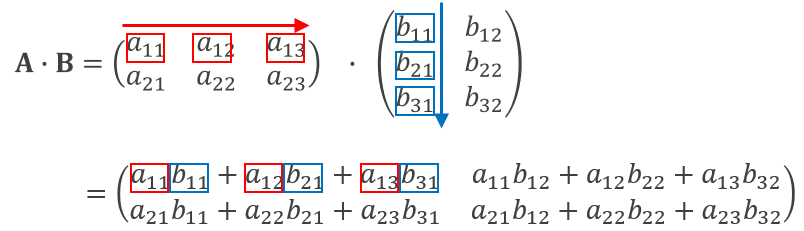
図11：行列の積 計算手順①
その他の成分も同様に、「行列Aを行方向」「行列Bを列方向」になぞるという方法は一貫したまま、なぞる位置をずらして計算しています。
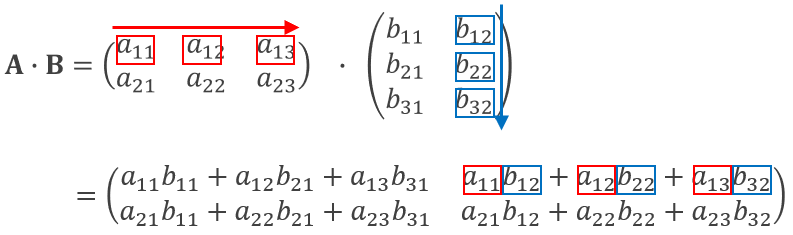
図12：行列の積 計算手順②
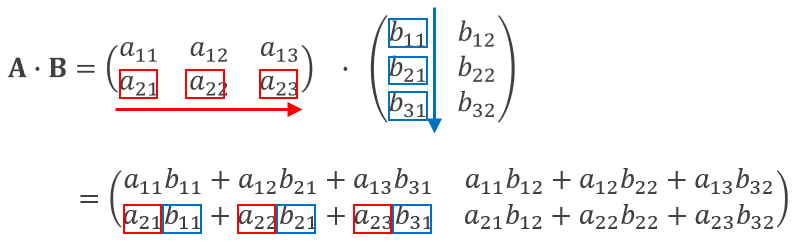
図13：行列の積 計算手順③
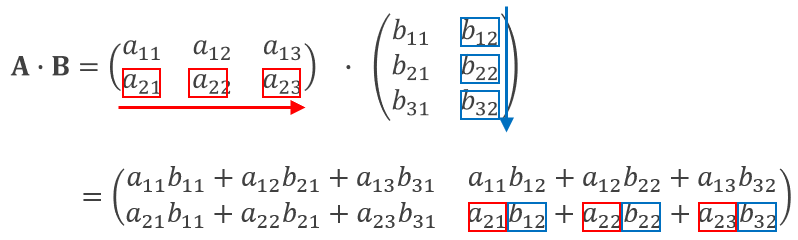
図14：行列の積 計算手順④
行列の大きさが変わっても、計算手順は変わりません。具体的な数値例を出して計算してみましょう。例えば3行3列の正方行列同士のかけ算をしてみます。
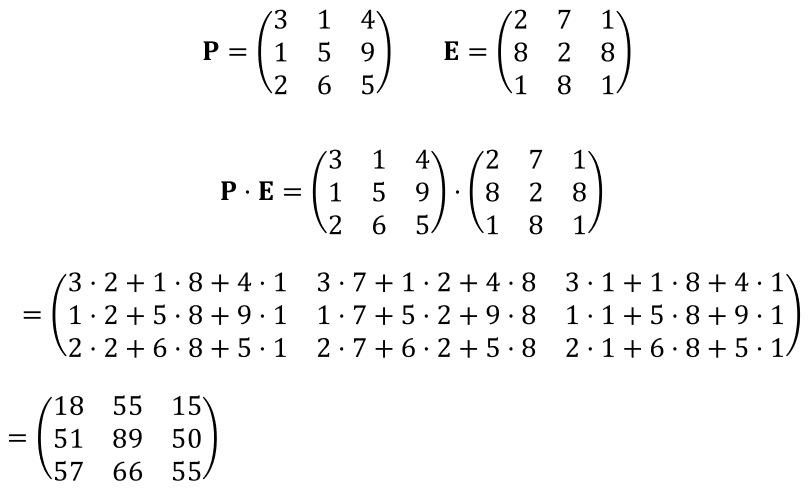
図15：行列の積 例題
さらに今度は、かけ算の順序を入れ替えて再度計算してみましょう。得られる答えは全く別のものになります（行列の積が非可換であることの実例）
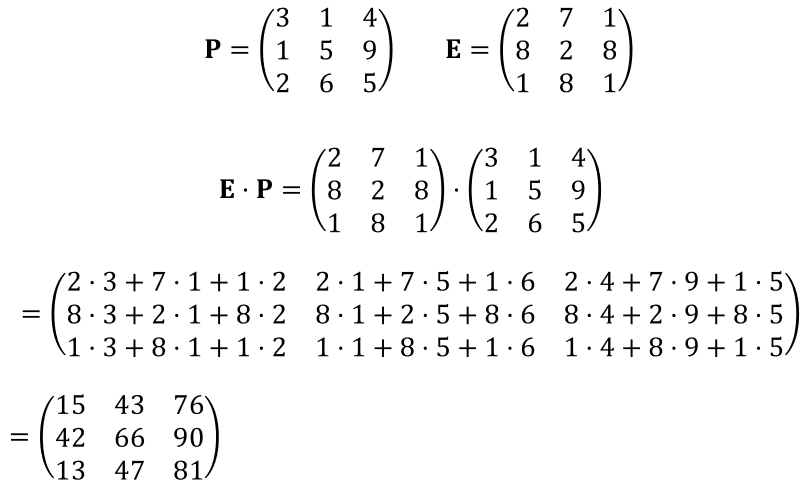
図16：席の順番を入れ替えると答えが変わる（非可換）
かけ算しても値が変わらない行列…単位行列
足し算・引き算しても値が変わらない行列を「零行列」といったように、かけ算しても値が変わらない行列が存在します。いわば、（普通の数値の）かけ算における１に相当する行列です。そのような行列を「単位行列」といい、記号Iで表します。（Eを使う場合もあります）
単位行列は「正方行列」で、対角成分（行列の左上から右下に向かった対角線上の成分）が１，それ以外の成分が０である行列です。
図17：単位行列の定義
具体例を使って計算してみましょう。確かにかけ算をしても答えが変わらない事が確認できます。
図18：単位行列をかけ算しても答えは変わらない
こちらも是非
“もっと見る” ブログ
センサーのすべてがわかる！組み込み技術者のための基礎知識
私たちの生活を豊かにするために欠かせないセンサー。そんなセンサーの仕組みや種類について、分かりやすく解説していきます。
ブラシレスモーター制御用MCUをささっと動かしてみよう！【RL78編】
私の主観としては、”モーター制御用途でも十分使用可能な超汎用MCU”です。現状最も人に勧められるMCUの1つです。2つめのリンク stmcu.jpは、ログインする事でリファレンスマニュアルやペリフェラルの使い方に関する日本語資料が閲覧できますので、ユーザー登録をおススメします。
【フーリエ級数編3：フーリエ級数展開】イメージでしっかりつかむ信号処理〜基礎から学ぶFFT〜
いよいよ、フーリエさんの発見したフーリエ級数展開を学んでいきます。『全ての周期信号は三角関数（サイン波・コサイン波）の足し合わせで表現できる』と言葉ではすでに説明しましたが、これを数式を使って定義すると、図のようになります。