フーリエさんの発見がもたらしたもの
フーリエさんの発見
さて、いよいよこの連載の本題である「フーリエ分析」の世界へと足を踏み入れていきましょう。
「フーリエ」というのは人の名前で、フルネームをジャン・バティスト・ジョゼフ・フーリエ男爵といいます。1768年にフランスで生まれた後孤児になり、幼少期から数学に興味を示しました。その後教会で修道士として修業をしながら、数学の勉強をつづけたのです。
さらにその後、大学の教授として数学や物理学の研究をする中で、フーリエは『全ての周期信号は三角関数(サイン波・コサイン波)の足し合わせで表現できる』という事を発見しました。当時としてはあまりにも斬新なアイデアだったため、発表した当初は議論を呼びましたが、この理論の重要性が後に理解され、広く使われるようになります。一次元信号のスペクトル分析の始まりです。
ここで「周期信号」という言葉が出てきました。周期的な信号、すなわち一定間隔ごとに同じ形を繰り返す信号のことです。多くの場合は時間信号、つまり横軸が時間軸となっている信号を扱うことが多いので、この場合の周期信号は「一定時間ごとに同じ形を繰り返す波形」という意味になります。この条件さえ守られていれば、形状の指定はありません。三角波や矩形波、パルス波のように直線で出来た波形でも、sin関数やcos関数のようななめらかな曲線はもちろん、ヘロヘロ・フラフラした何とも言えない形であっても、一定時間ごとに同じ形が繰り返されていれば周期信号です。
逆に「非周期信号」は、例えば短時間だけ信号が変化し、その前後で全く信号が変化しない「単発波形」や、ランダムな上下を繰り返す「(ホワイト)ノイズ」などがあります。
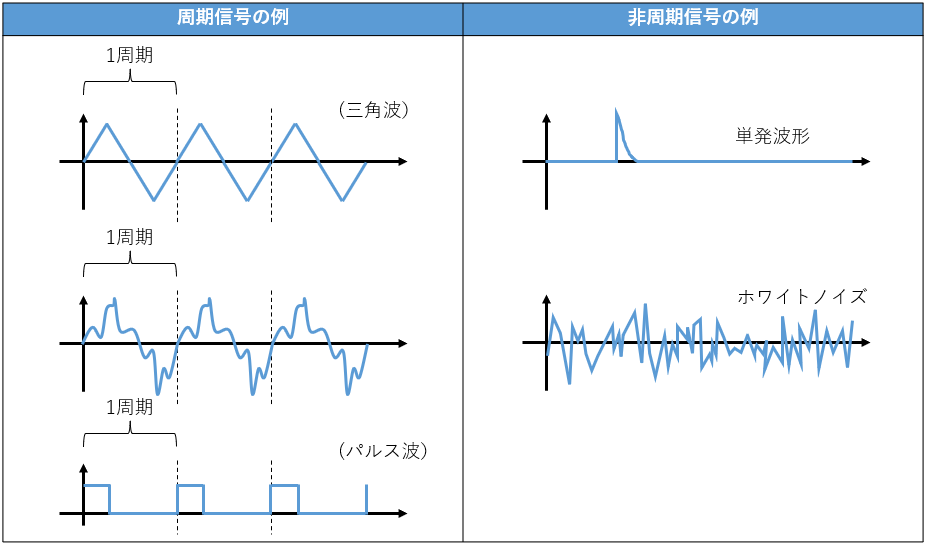
図1:周期信号と非周期信号
音と調波構造
一次元の時間信号で代表的かつ身近な例は音です。
音というのは、物体の振動(振動源)により周囲の空気(媒体)が震え、その振動が耳の中の鼓膜から内耳、脳の聴覚野に伝わって感じられる情報です。従って音は、空気圧の時間変化をとらえた信号(音波信号)として考えることができます。
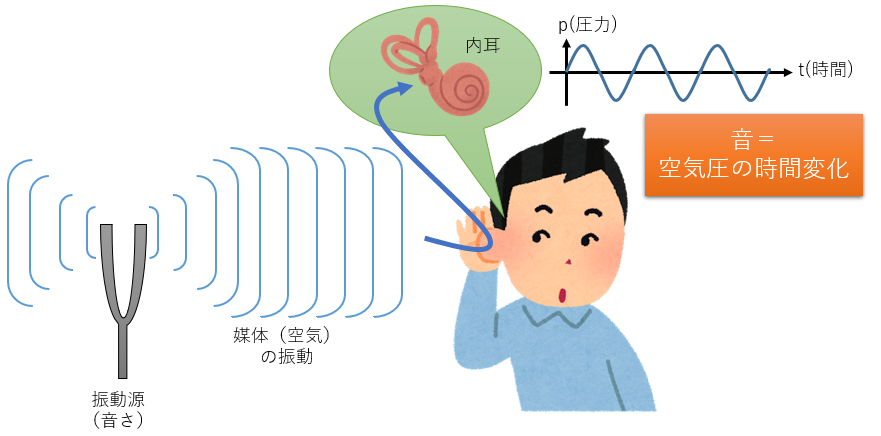
図2:物理現象としての音
楽器の音を考えてもらうと分かりやすいのですが、バイオリンやフルートのような楽器の音は、はっきりと音の高さ(ピッチ)を知覚できます。このような音を「有ピッチ音」と言ったりします。一方、小太鼓(スネア)を叩く音は音の高さを知覚することがほとんどできません。このような音は「無ピッチ音」と言います。「有ピッチ音」と「無ピッチ音」の違いはどこにあるのでしょうか。それは音の波形を周波数成分に分割する(スペクトルを求める)とわかります。
「有ピッチ音」は、ある基準となる周波数のサイン波・コサイン波(基本周波数(成分)または基音という)と、その2倍・3倍・4倍…という整数倍の波(高調波(成分)または倍音という)が混在してできています。このような構造を「調波構造」といいます。これはまさにサイン波・コサイン波の足し合わせが行われているという事であり、音波信号が周期波形であることを意味します。
音の分解や合成
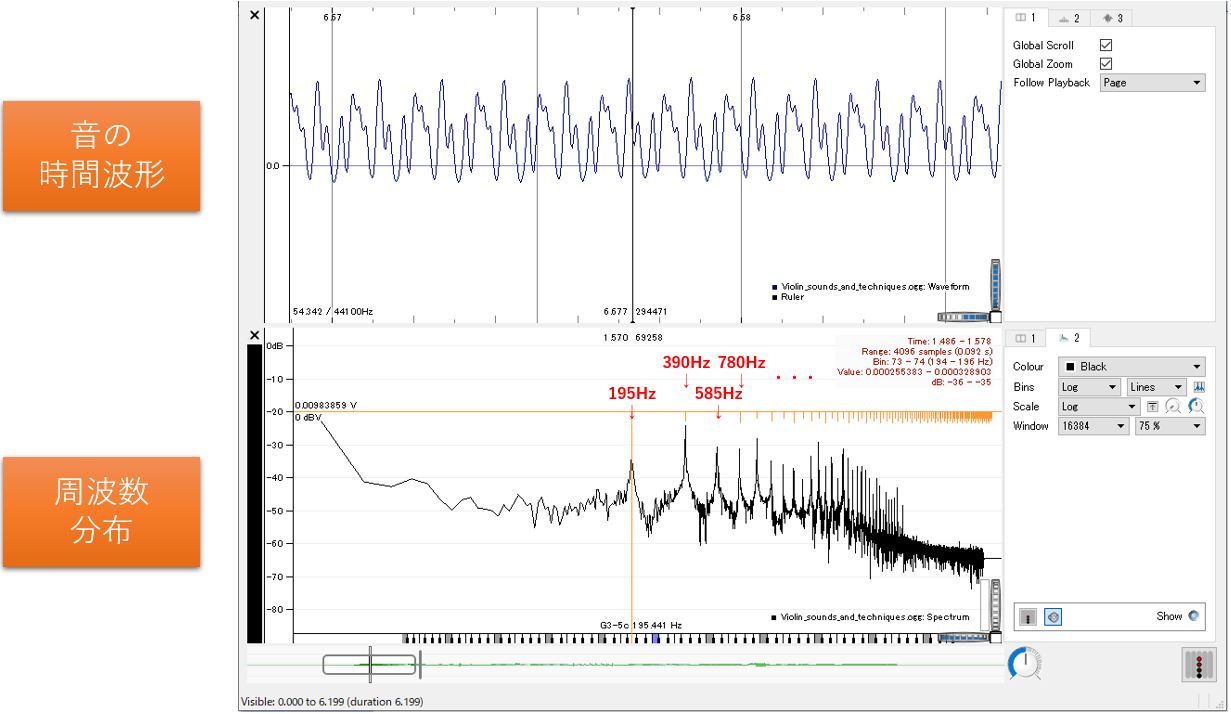
図3:バイオリン音の分析
上の図を見て下さい。これはWikimedia Commonsで公開されているバイオリン音源「 Violin sounds and techniques.ogg」の開始約6.6秒の部分を分析したものです。分析には「 Sonic Visualiser」というツールを使用しました。
図の上部は、音の時間波形(横軸が時間、縦軸が圧力)を表しています。図の下部は、この音をフーリエ分析(より正確にはFFT)によって周波数ごとに成分を分解した周波数分布(横軸が周波数、縦軸がパワー)を表しています。つまり本連載の最終目標は、図上部の時間波形から、図下部の周波数分布を求める方法を理解することです。
時間波形を見ると、似たような形の波形が繰り返されている、まさに周期波形であることが読み取れるかと思います。周波数分布を見ると、いくつもの山がある、いわゆる「くし形」の形状をしています。この山が示す周波数を確かめると、一番低周波の山が約195Hz(低いソの音に相当)で、これが基音に相当します。そしてその上の山は390Hz、585Hz、780Hz…と、基音の2倍・3倍・4倍…の周波数になっており、調波構造になっていることがわかります。
ちょっと余談:分解できるなら、再現もできる
上述のバイオリンの音を「料理」とするならば、フーリエ分析はその料理から「基音・倍音」という食材と、その「パワー」という混合比率(レシピ)を求めることに相当します。
ということは逆に、求めた「食材」と「混合比率(レシピ)」がわかれば、「料理」(=楽器音)が得られることは容易にイメージできると思います。
音楽演奏用に合成音を作る装置のことをシンセサイザーといいますが、「基音・倍音」に相当するサイン波をたくさん足して音を作る方式は、シンセサイザーの最も原始的かつ基本的な手法(加算合成方式)です。

図4:初期のシンセサイザ(モーグ・シンセサイザ)
声の分析
楽器音だけでなく声もまた音の一種であり、分析すると大変幅広く応用できます。
人間の声には個人差があり、声(音)に差があるということは、その周波数成分に違いがあるということです。人間の声を周波数分析したものを俗に「声紋」といい、この声紋に現れる個人差を識別することで、話者認識や個人認証(声紋認証)が可能になります。
それとは逆に同じ文章を読み上げた多数の音声から「個人差」に相当する部分を引き算していくと、最後まで残った特徴はその文章に固有の特徴であるはずです(例えば〈こんにちは〉という文章の音声から、個人差を除いていけば、最後に残るのは〈こんにちは〉という文章そのものが持っている特徴と考えられます)。
下の図は、元気で明るい女性の声( 効果音ラボ 声素材―アプリ・音声案内(元気な女の子)→「おめでとうございます」)と、アナウンス風で落ち着いた女性の声( 効果音ラボ 声素材―アプリ・音声案内(落ち着いた女性)→「おめでとうございます」)による「おめでとうございます」という音声の波形(画面上部)と声紋(スペクトログラム、画面下部)を表示したものです。分析には「Sonic Visualiser」というツールを使用しました。声が違うので声紋が異なる一方で、同じ文章を読んでいるため全体的な特徴が似ていることも何となくわかってもらえるでしょうか。
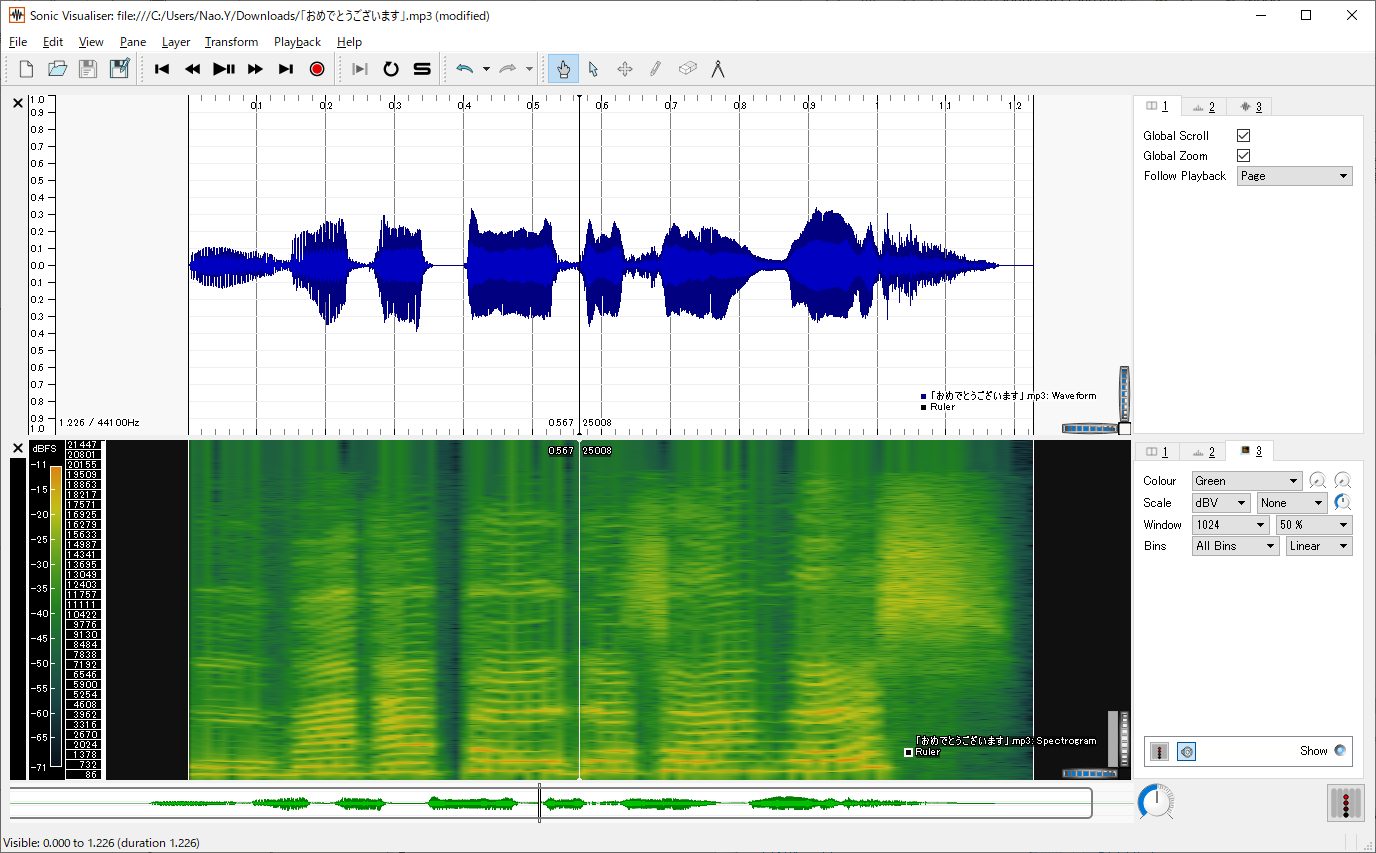
図5:元気で明るい女性の〈おめでとうございます〉
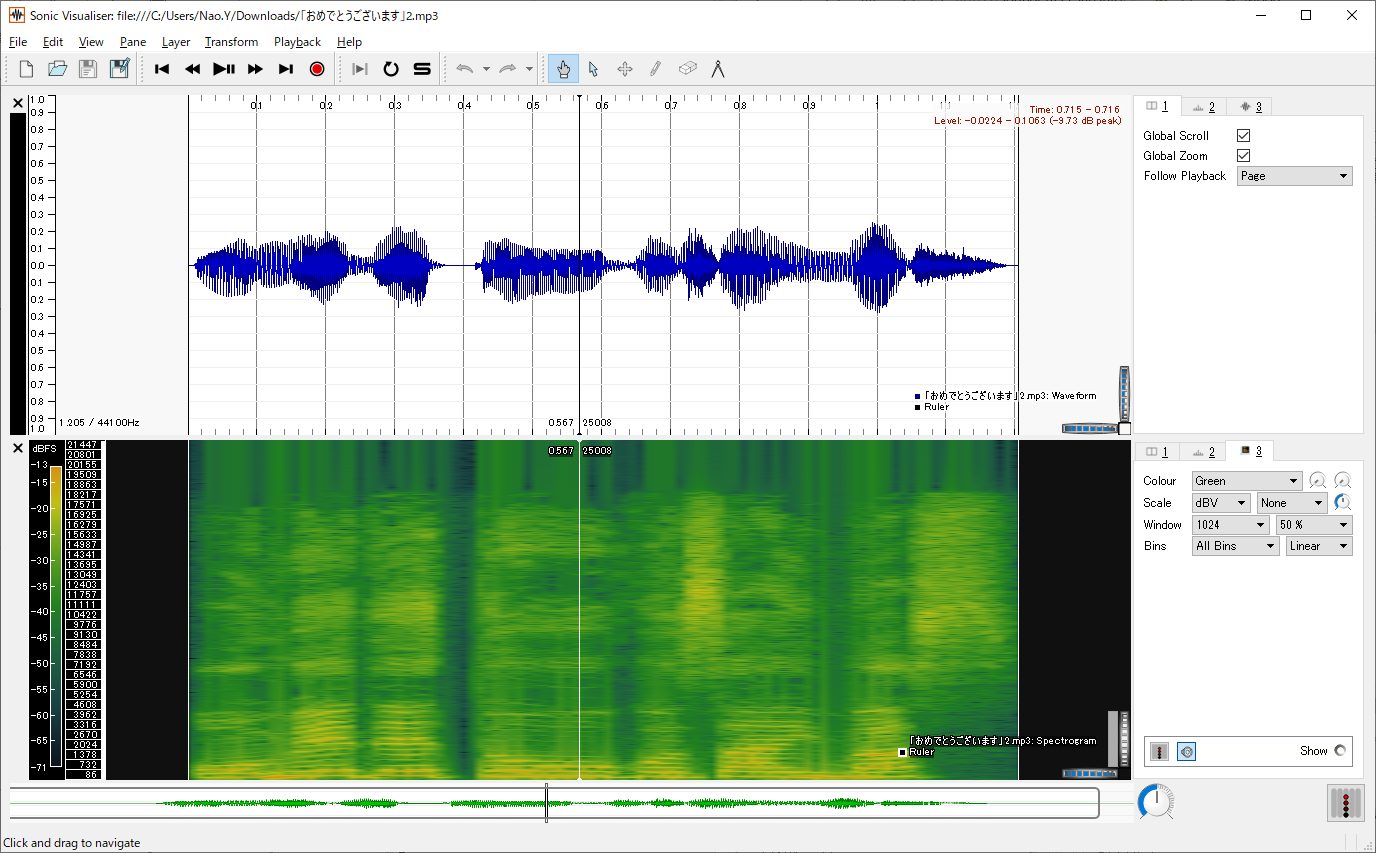
図6:アナウンス風で落ち着いた女性の〈おめでとうございます〉
フーリエ級数展開とその仲間
フーリエさんの発見(『全ての周期信号は三角関数(サイン波・コサイン波)の足し合わせで表現できる』)は、後に「フーリエ級数(展開)」と名付けられます。
フーリエ級数は革新的な発見でしたが、取り扱える信号が「連続信号」かつ「周期信号」に限られるという制約がありました。その制約を取り払うべくフーリエ級数は発展し、数多くの仲間を作ります。
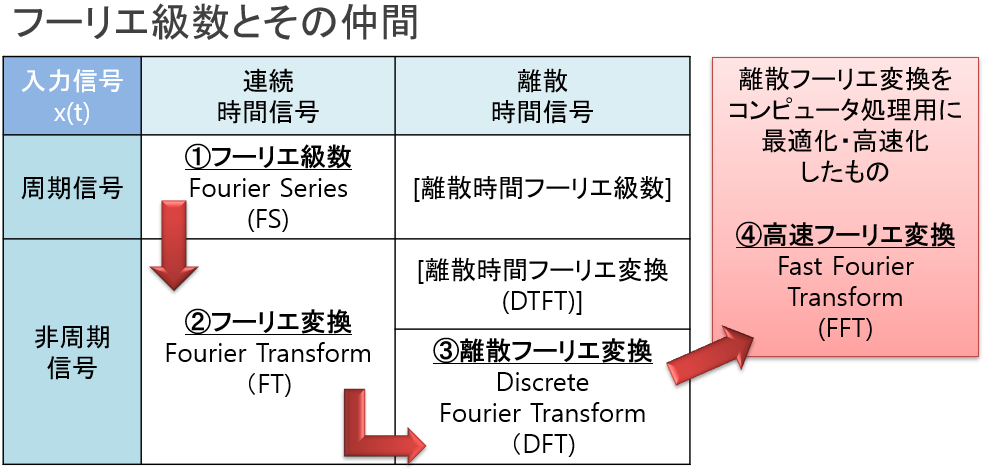
図7:フーリエ級数とその仲間
この連載では、(ほぼ)歴史の流れに沿って、①フーリエ級数展開(FS)→②フーリエ変換(FT)→③離散フーリエ変換(DFT)→④高速フーリエ変換(FFT)という流れで話を進めていきます。
これらはすべて入力信号から周波数成分を求める処理になります。それとは逆に、周波数成分から信号を求める「逆変換」も存在しますが、逆変換については簡単に紹介するのみで、詳しくは扱いません。
こちらも是非
“もっと見る” ブログ
はじめての耐量子暗号
量子コンピューティングはさまざまな面で明るい未来のために期待される技術である反面、その演算能力をセキュリティ上の攻撃に使われることを考えると、既存の暗号技術にとって深刻な脅威でもあります。
Arm®対応のWindows IoT OS 【Windows IoT on Arm】を評価ボードで動かしてみる
組み込み機器向けOS、Windows 10/11 IoT Enterprise(以下Windows IoT)がサポートするArmプラットフォームが拡大しています。Windows IoT on Armは、Windows IoTのメリットそのまま、より低コストで低消費電力というArmならではのメリットもございます
【フーリエ級数からフーリエ変換へ:フーリエ変換編1】イメージでしっかりつかむ信号処理〜基礎から学ぶFFT〜
ここまで学んできたフーリエ級数展開は、「入力信号が周期波形でなければならない」という制約がありました。上図のような太鼓の音、すなわち単発波形は、フーリエ級数展開できないのでしょうか














