フーリエ級数展開と角周波数
フーリエ級数展開の公式(基本編)
いよいよ、フーリエさんの発見したフーリエ級数展開を学んでいきます。『全ての周期信号は三角関数（サイン波・コサイン波）の足し合わせで表現できる』と言葉ではすでに説明しましたが、これを数式を使って定義すると、図のようになります。
図1：フーリエ級数展開の定義式
いきなりヘビーな数式が出てきた！と恐れないで下さい。全体をまとめて理解しようとするのではなく、部分部分の意味を切り分けながら理解すると、それほど難しい事は書いていません。この式の意味は後ほど解説します。
角周波数の導入
フーリエ級数展開の式は、「角周波数」という表現方法を導入するともう少しわかりやすくなります。角周波数は「波形の周期(繰り返し時間)」と「円上を一定速度で回転する点」を 波形の1周期＝点の1回転 として結び付け、波形の周波数を円上の点が移動する回転速度として表現したものです。
拡張された三角関数は、単位円上にある点の座標を使ってsinとcosを定義しました。この点が一定速度で反時計回りに回転すると考えて、x,y座標の値をグラフ化すると、sinカーブとcosカーブが得られます。
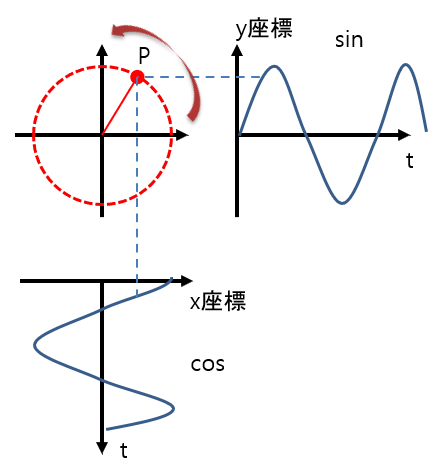
図2：単位円上を回転する点とsin, cos波の関係
単位円上の点Pがぐるりと1周すると、sinカーブとcosカーブもちょうど１周期進んで元の位置に戻ってきます。点Pとx軸の成す角度をθとしたとき、点Pの1回転（θ＝0～2π）が波形の1周期に相当します。従って、回転速度が速くなれば、sinカーブ・cosカーブの1周期も短時間になる（＝周波数が高くなる）ことになります。両者は1対1で結びついた関係なので、sinカーブ・cosカーブの周波数は点Pの回転速度として表現できることになります。これを「角周波数」といいます。
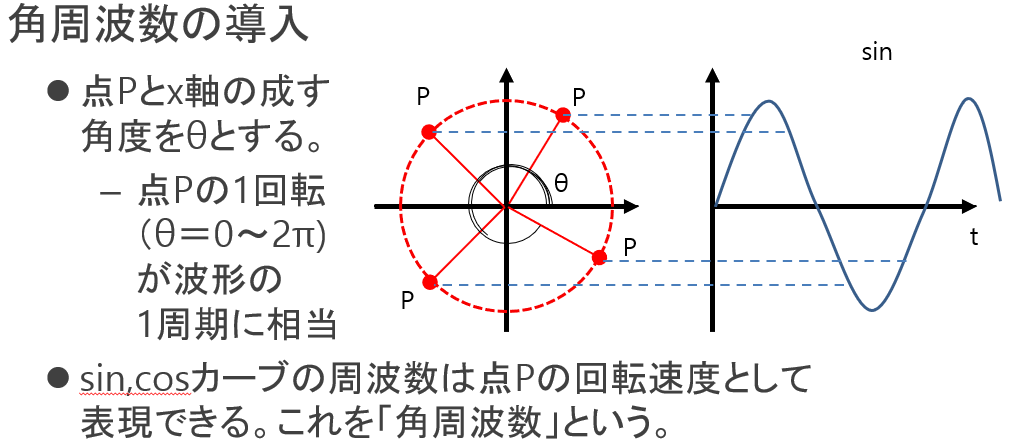
図3：角周波数の導入
角周波数は通常、記号ω（オメガ）で表し、波形の周期または周波数がわかれば簡単に計算できます。単位は[rad/sec]、すなわち点Pが1秒間に何[rad]進むかを表しています。
図4：角周波数の定義式と意味
例えば、ピアノ中央のラの音は周波数440[Hz]ですので、角周波数で表すと880π[rad/sec]となります。要するに、点Pが単位円上1秒間に440回転する×1周は2π[rad]＝点Pが1秒間に880π[rad]回転するという意味です。
フーリエ級数展開の公式(角周波数編)
フーリエ級数展開の定義式をよく見ると、角周波数が中に隠れています。そこを取り出して角周波数の記号ωに置き換えると、図のようになります。
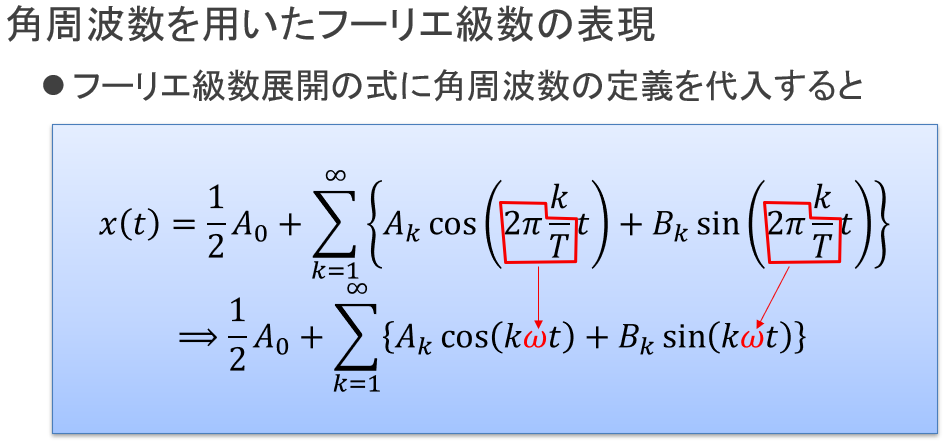
図5：フーリエ級数展開に角周波数を導入
角周波数を導入することで、フーリエ級数展開の定義式が、少しではありますがすっきりしました。
フーリエ級数展開の式を眺める
ここからはフーリエ級数展開の公式を切り分けながら眺め、式の意味を理解していきます。
総和記号（Σ）の外に飛び出している項にまずは注目します。この式ではtが時間を表す変数になっていますが、この項には変数tが存在しません。つまりこの値は時間によって変化しません。このフーリエ級数が表す波形を全体的に押し上げたり（プラスの場合）引き下げたり（マイナスの場合）するだけの成分です。これは周波数0[Hz]（＝時間によって変化しない）の成分と考えて下さい。正式名称は「直流成分」といいます。
図6：フーリエ級数の式を眺める(1)
総和記号（Σ）の読み方はすでに説明した通りです。和を求めるためのループ変数kを0で初期化し、無限大まで1つずつ増やしながら合計していく事を意味します。
ωは上で説明した角周波数を表しています。元信号（このフーリエ級数で表現される波形）の周期または周波数から求められます。
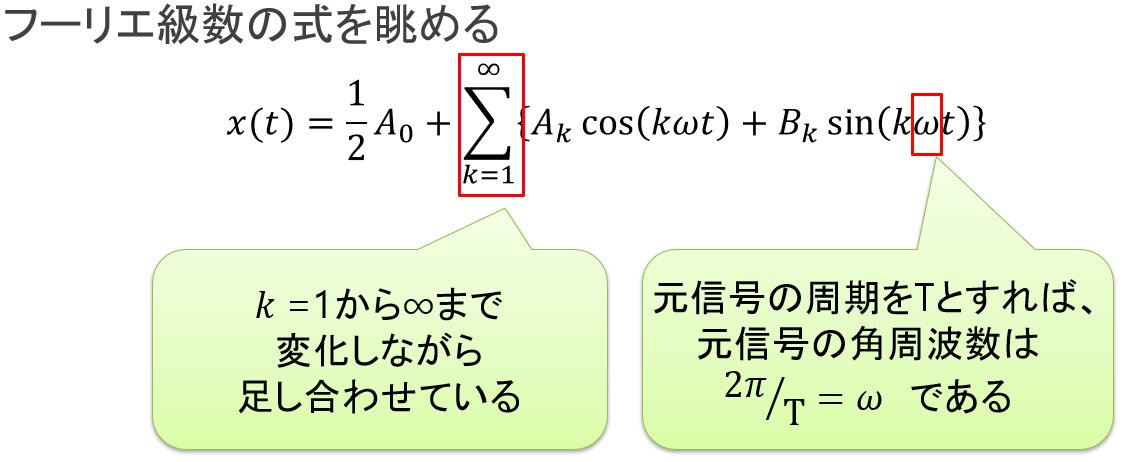
図7：フーリエ級数の式を眺める(2)
元信号の角周波数ωと、Σによって順に変化していくループ変数kがかけ算されたkωは、元信号の1倍・2倍・3倍…の（角）周波数を意味します。
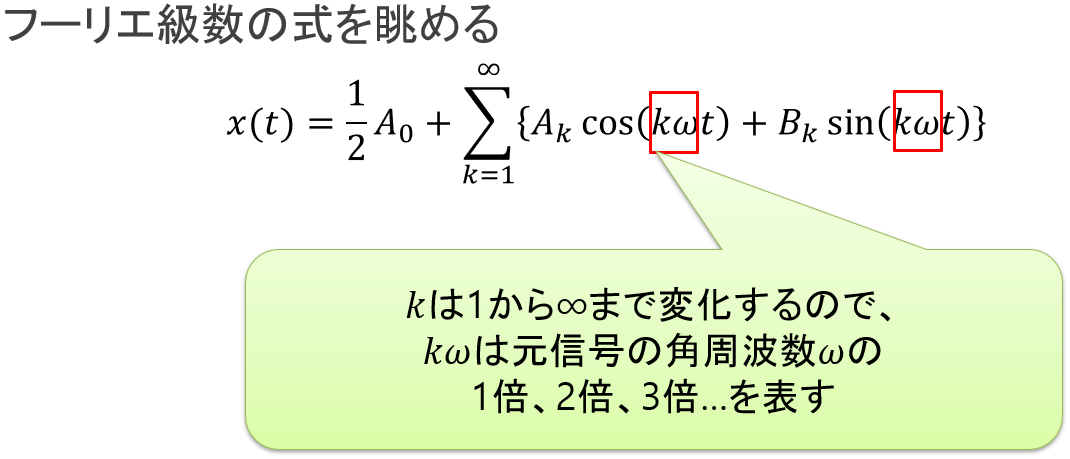
図8：フーリエ級数の式を眺める(3)
そのkωが、時間を表す変数tと共にcos関数とsin関数の中に入る事で、周波数kωのcos波とsin波を表します。
図9：フーリエ級数の式を眺める(4)
cos波とsin波の大きさは±1で固定です。これに係数列Ak､Bkがかけ算されると、それぞれの波の大きさが変化します。
つまりΣの中は、元信号の1倍・2倍・3倍…の（角）周波数を持つcos波、sin波を、係数列Ak,Bkで表される大きさ（比率）で混ぜ合わせている（混合加算）ことになります。
図10：フーリエ級数の式を眺める(5)
具体例を考えてみましょう。ｋが1から無限大まで変化するのを「具体的」に考えるのは難しいので、k=１～３までで打ち切ることにして、図のような前提条件を考えます。
図11：フーリエ級数による波の表現 例１（前提条件）
直流成分（A0の項）は一旦無視して、先に総和記号Σを片付けます。
係数A1,A2,A3…が全て０なので、総和の中に入っているcosの項は全て0となり、無視することができます。また係数B4以降も全て0なので、無視することができます。総和記号Σをやめて、式を展開すると以下のようになります。
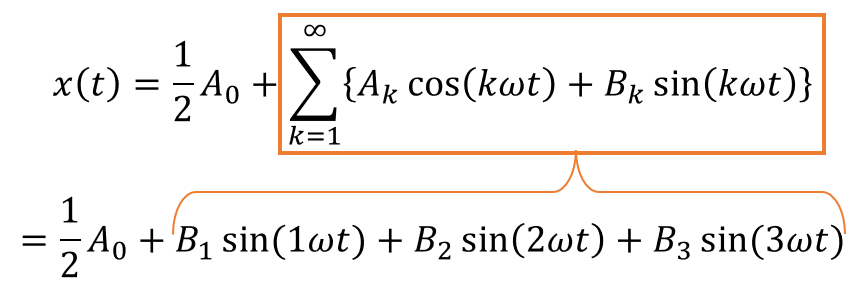
図12：フーリエ級数による波の表現 例１（導出1）
A0,B1～B3,ωに前提条件の値を入れて整理します。
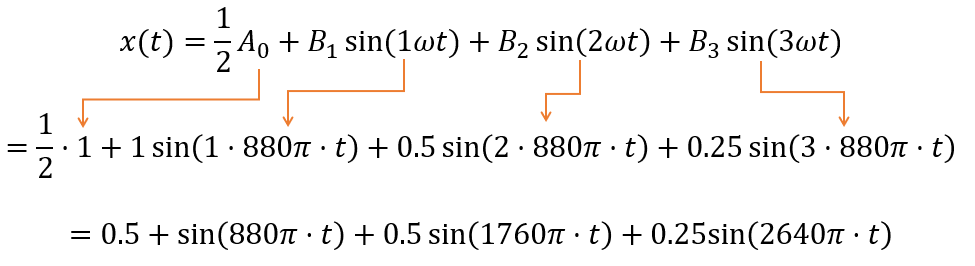
図13：フーリエ級数による波の表現 例１（導出2）
それぞれの項をグラフにすると、直流成分、1倍・2倍・3倍の角周波数を持つ波の合計になっていることがよくわかります。
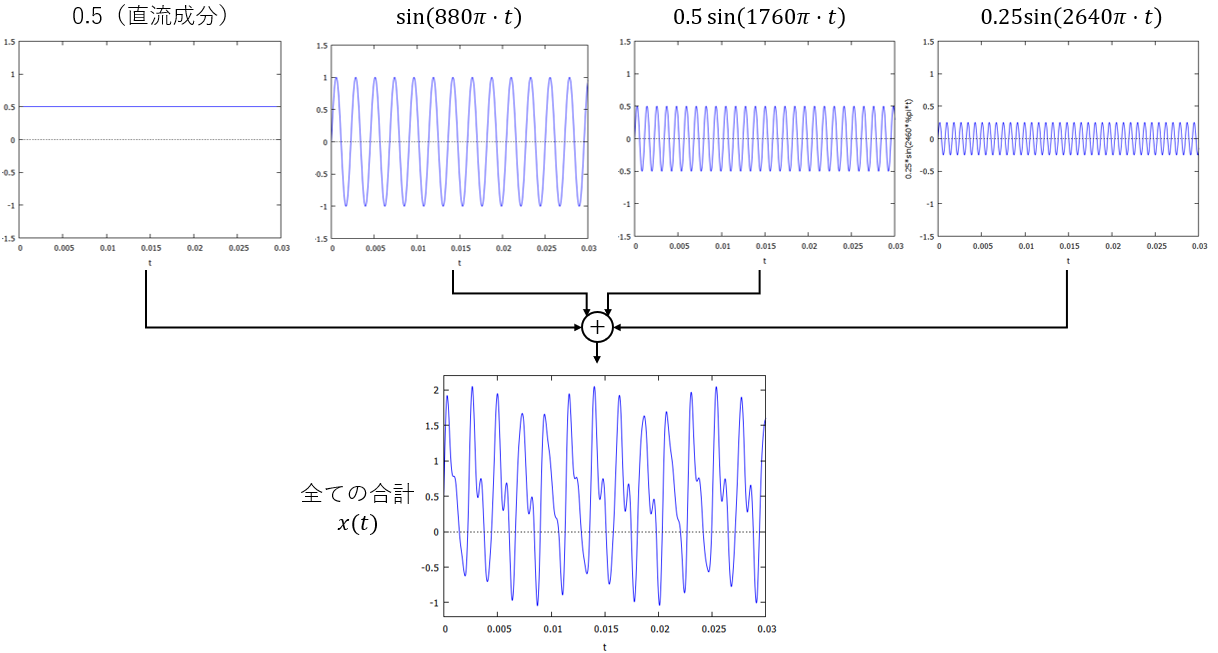
図14：フーリエ級数による波の表現 例１（図示）
もう一つ例を考えてみましょう。今度はk=１～２までしかなく、直流成分がない代わりにsinとcosが混在します。
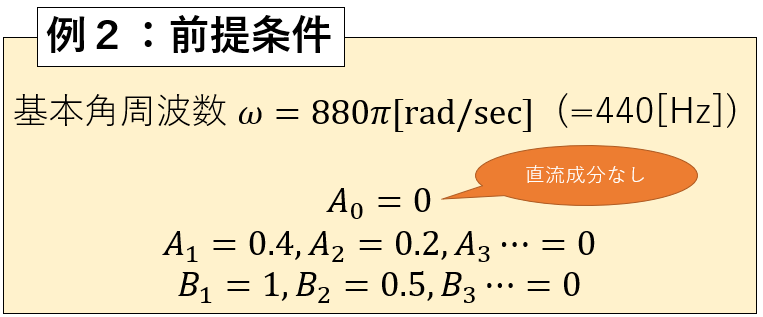
図15：フーリエ級数による波の表現 例2（前提条件）
直流成分（A0の項）は明らかにゼロなので消してしまい、総和記号Σを片付けます。
係数A3以降とB3以降は全て0なので、無視することができます。総和記号Σをやめて、式を展開すると以下のようになります。
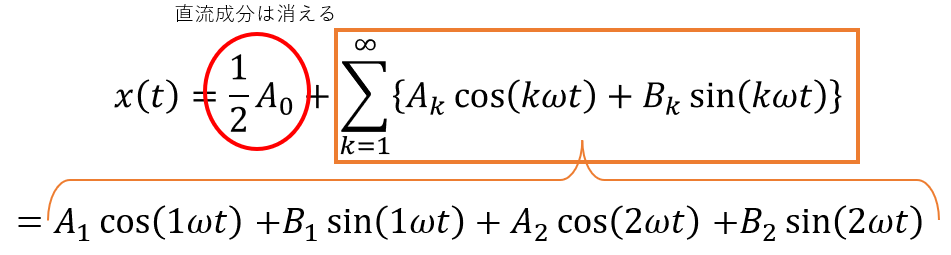
図16：フーリエ級数による波の表現 例2（導出1）
A1～A2,B1～B2,ωに前提条件の値を入れて整理します。
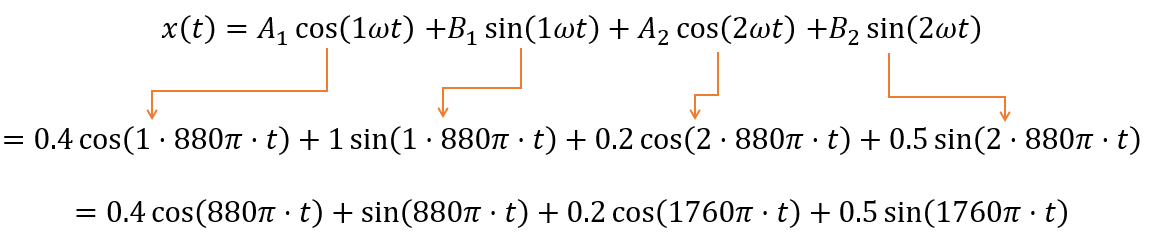
図17：フーリエ級数による波の表現 例2（導出2）
それぞれの項をグラフにしてみます。1倍・2倍の角周波数を持つsin波とcos波の合計になっています。
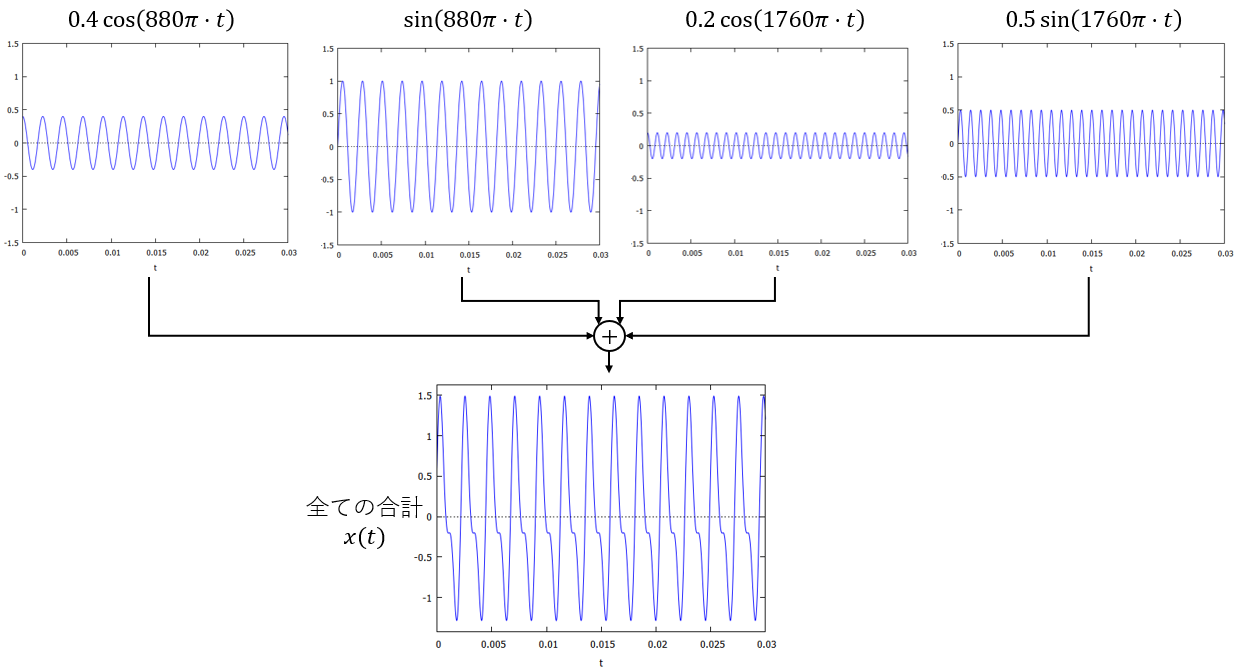
図18：フーリエ級数による波の表現 例2（図示）
このように、ω、A0、Ak、Bkを様々に変化させることで、あらゆる周期波形を表現できる、というのがフーリエ級数展開の主張です。
基本波と高調波
フーリエ級数展開では、角周波数ωとその2倍・3倍…の角周波数を持つ成分が登場しますが、これにはそれぞれ名前があります。
特に「高調波」と「高調波成分」は混乱しがちなので注意しましょう。
図19：基本波と高調波
時間領域表現と周波数領域表現
通常、音の波形を示すときは横軸が時間tで、縦軸が振幅（信号の大きさ）になっているグラフを使用します。このような信号の表し方を、時間（領域）表現といいます。
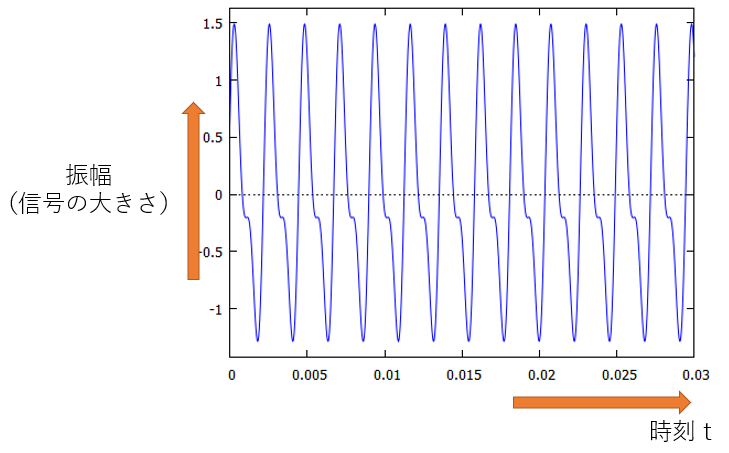
図20：信号の時間領域表現
一方、フーリエ級数展開によって、周期波形は基本波と高調波の混合比率で表現することができるようになりました。そのため、横軸を周波数ｆ、縦軸を混合比率（成分の大きさ）で表すことができます。このような表現を周波数領域表現といいます。スペクトル、またはスペクトラムともいいます。
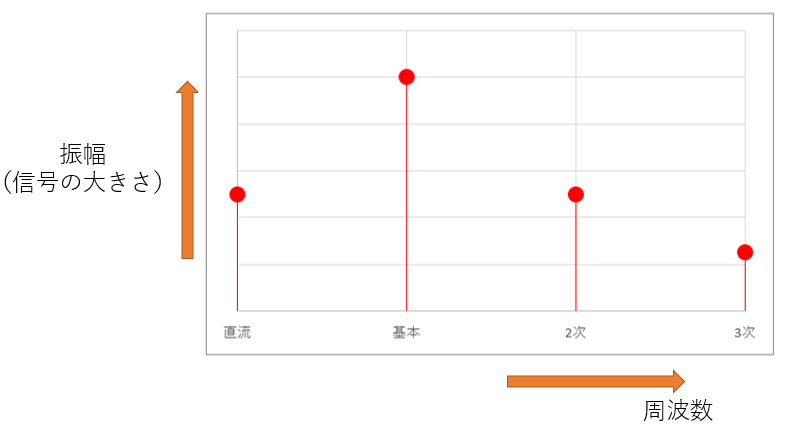
図21：信号の周波数領域表現
ちょっと余談： Maximaでグラフを描く
図で使用している関数のグラフはMaximaを使って描いています。Maximaに以下のコマンドを入力すると、グラフが描画できます。
【例１】
直流成分
plot2d(0.5,[t,0,0.03],[y,-1.5,1.5]);
基本波
plot2d(sin(880*%pi*t),[t,0,0.03],[y,-1.5,1.5]);
2次高調波
plot2d(0.5*sin(1760*%pi*t),[t,0,0.03],[y,-1.5,1.5]);
3次高調波
plot2d(0.25*sin(2460*%pi*t),[t,0,0.03],[y,-1.5,1.5]);
合計
plot2d(0.5+sin(880*%pi*t)+0.5*sin(1760*%pi*t)+0.25*sin(2460*%pi*t),[t,0,0.03]);
【例２】
基本波（cos）
plot2d(0.4*cos(880*%pi*t),[t,0,0.03],[y,-1.5,1.5]);
基本波（sin）
plot2d(sin(880*%pi*t),[t,0,0.03],[y,-1.5,1.5]);
2次高調波（cos）
plot2d(0.2*cos(1760*%pi*t),[t,0,0.03],[y,-1.5,1.5]);
2次高調波（sin）
plot2d(0.5*sin(1760*%pi*t),[t,0,0.03],[y,-1.5,1.5]);
合計
plot2d(0.4*cos(880*%pi*t)+sin(880*%pi*t)+0.2*cos(1760*%pi*t)+0.5*sin(1760*%pi*t),[t,0,0.03]);
こちらも是非
“もっと見る” ブログ
センサーのすべてがわかる！組み込み技術者のための基礎知識
私たちの生活を豊かにするために欠かせないセンサー。そんなセンサーの仕組みや種類について、分かりやすく解説していきます。
ブラシレスモーター制御用MCUをささっと動かしてみよう！【RL78編】
私の主観としては、”モーター制御用途でも十分使用可能な超汎用MCU”です。現状最も人に勧められるMCUの1つです。2つめのリンク stmcu.jpは、ログインする事でリファレンスマニュアルやペリフェラルの使い方に関する日本語資料が閲覧できますので、ユーザー登録をおススメします。
【フーリエ級数編2：世界で最も美しい数式】イメージでしっかりつかむ信号処理〜基礎から学ぶFFT〜
角度を表すとき、私たちは一般に円一周を360分割して単位[°]をつけた度数法を使用しています。数学の世界では度数法ではなく、弧度（こど）法という角度表現を用いることが一般的です。弧度法の単位は[rad]で、ラジアンまたはラディアンと読みます。円一周の角度を2π[rad]と定義する表現方法で、これは半径が１である円（単位円）をある角度で扇形に切り取ったとき、その中心角度を切り取った扇の外周の長さで表現する事に相当します。
