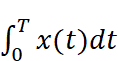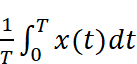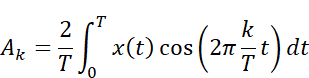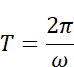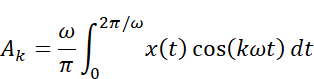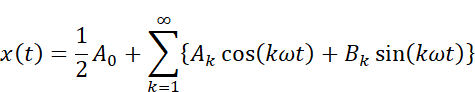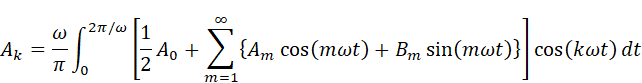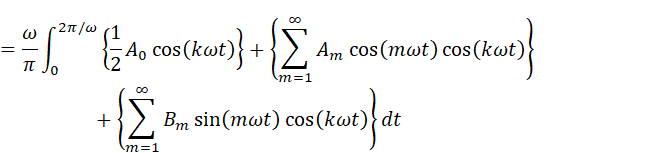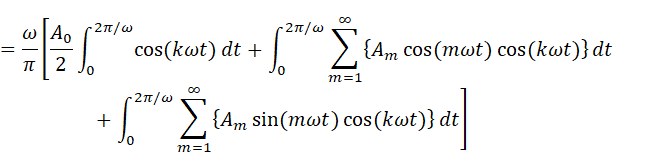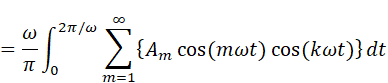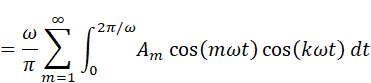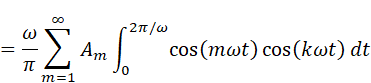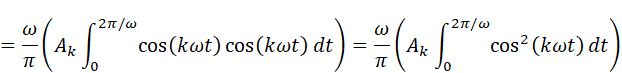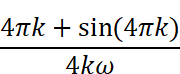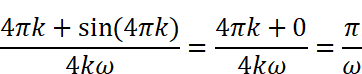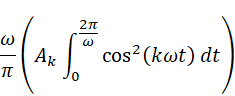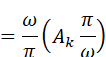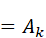任意の関数を再現するフーリエ係数を求める
フーリエ係数は求められるのか
前回の記事（フーリエ級数編３）で、フーリエ係数Ak（直流成分となるA0も含みます）, Bkを定めれば、様々な周期波形がフーリエ級数の式によって表現できるということを説明しました。（図１）
図1：フーリエ級数展開の定義式【再掲】
では、フーリエ級数で表現したい信号x(t)があるとして、そのx(t)をうまく再現してくれるようなフーリエ係数Ak, Bkを求めることはどうすればできるのでしょうか。
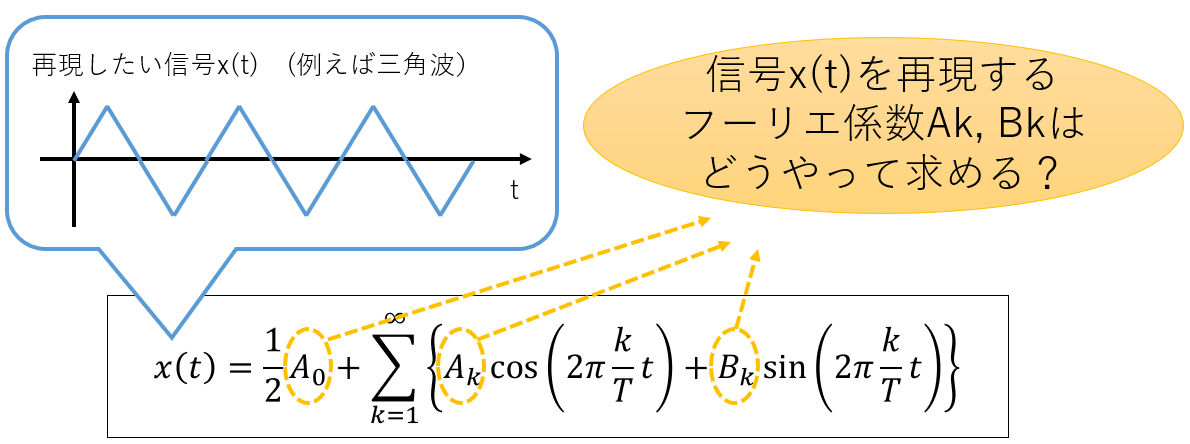
図2：フーリエ係数を求めたい
結論から言えば、もちろん求めることができます。そのためには「（三角）関数の直交性」という性質が大活躍します。（結論だけ知りたい、と言う人は後ろの「フーリエ係数とスペクトルを求める」まで読み飛ばしてください）
（三角）関数の直交性
「直交」という言葉は多くの人が聞いたことがあるでしょう。
最もなじみがあってわかりやすいものは、幾何学（図形の数学）における「直交」でしょう。これは互いに交わる2つの直線や平面の成す角度が直角（90°）であることを意味します。
ベクトルにおける「直交」は、2つのベクトルの「内積」という計算をした時に、値が0になる事を意味します。この定義は、幾何学の「直交」を拡張したものです。ベクトルを2次元平面や3次元空間上の直線とみなした場合は幾何学の「直交」と同じ意味になります。
そして、関数も（無限次元の）ベクトルとみなすことができ、内積を計算することができます。難しくなるので詳しくは触れませんが、異なる2つの関数f(x)とg(x)の内積が0になるとき、関数f(x)とg(x)は「直交」しているといいます。
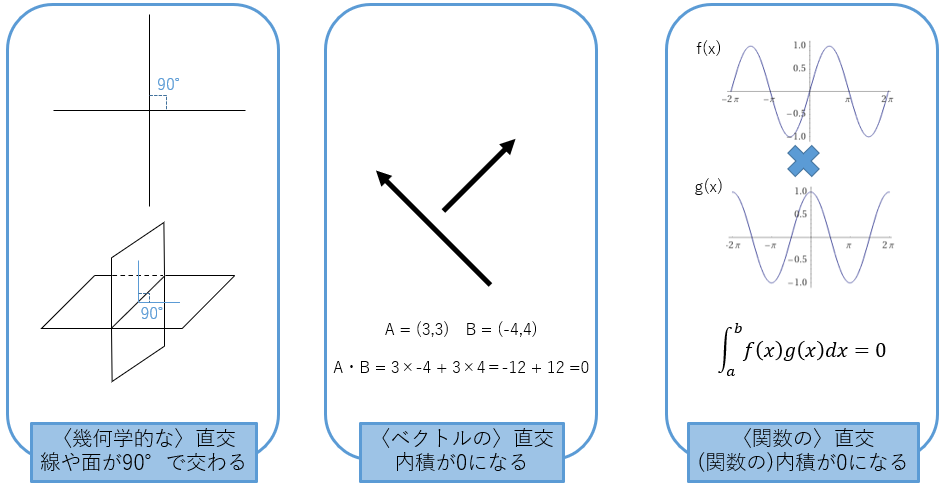
図3：3つの「直交」
三角関数sin(x)とcos(x)は、「直交（する）関数」の代表的な例です。この2つが直交しているため、以下のような面白い公式が成り立ちます。
図4：三角関数の直交性
この、「三角関数の直交性」を活用することで、任意の（周期）波形を再現するフーリエ係数を求めることができるのです。
ちょっと余談：三角関数を使用しないフーリエ級数（のようなもの）
三角関数（sin, cos）の他にも直交する関数は存在するので、そのような関数を使えば三角関数を使用しないフーリエ級数（のようなもの）を定義することが可能です。興味のある人は、 長沼 伸一郎『物理数学の直観的方法―理工系で学ぶ数学「難所突破」の特効薬〈普及版〉』を読んでみてください。フーリエ級数だけでなく、理解することがちょっと難しい様々な数学のトピックスについて、大変個性的で面白い解説をしてくれている良著です。
Wolfram Alphaを使って、三角関数の直交性を確認してみましょう。
まずはsinとcosの積です。変数m,nの値を{1,2}にした全組み合わせ（4通り）を計算してみます。積分の命令Integrateを使用して計算すると、以下のような結果になります。上で説明した通りの結果が得られています。
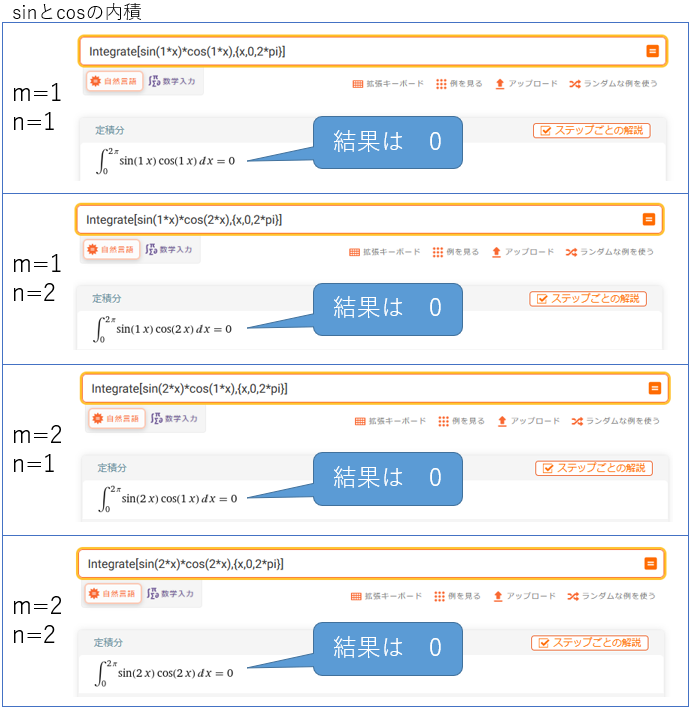
図5：WolframAlphaで三角関数の直交性を確認する(1)
図6：WolframAlphaで三角関数の直交性を確認する(2)
図7：WolframAlphaで三角関数の直交性を確認する(3)
Maximaでも計算が可能です（Maximaの場合、円周率piには、定数を表す記号%を先頭につける必要がある事に注意して下さい）。Maximaの場合は以下のように入力します。
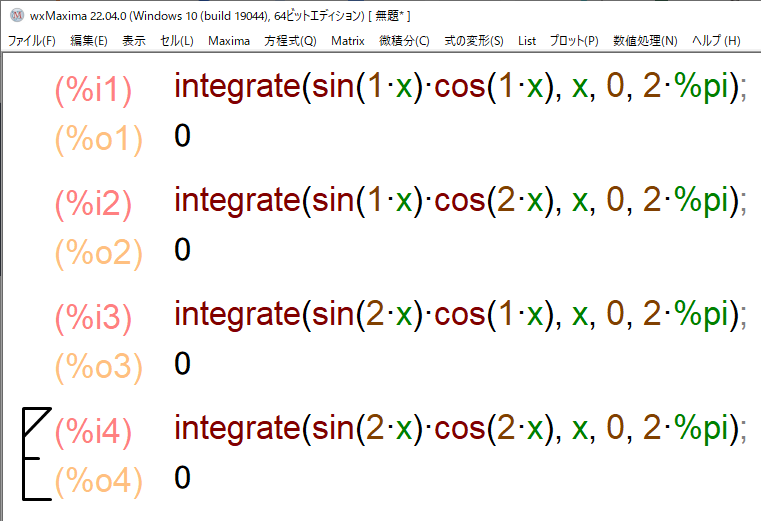
図8：Maximaで三角関数の直交性を確認する(1)
図9：Maximaで三角関数の直交性を確認する(2)
図10：Maximaで三角関数の直交性を確認する(3)
フーリエ係数とスペクトルを求める
フーリエ係数を、A0（直流成分）、Ak（cosにかかる係数）、Bk（sinにかかる係数）に分けて計算します。
フーリエ係数の公式
フーリエ係数を求める公式は以下の通りです。
図11：フーリエ係数の公式
難しいことはいいからとりあえず先に進みたい！という人は、「この公式で求められるんだ」ということだけ眺めてもらえれば良いと思います。ただ、順を追って理解すればそれほど難しい式でもないので、チャレンジしたい方は末尾につけた付録でぜひこの公式をもう少し掘り下げ、読み解いてみましょう。
スペクトルを求める
公式によって関数x(t)のフーリエ係数、A0・Ak・Bkを求めることができるわけですが、実用的にはこのAk, Bkの値から「振幅スペクトル」「位相スペクトル」「パワースペクトル（エネルギースペクトル）」という値を求め、これをx(t)の周波数分析結果とすることが多いです。
これは、Akを複素数の実部、Bkを複素数の虚部とみなしたとき、その複素数の絶対値が振幅スペクトル、偏角が位相スペクトル、振幅スペクトルの2乗がパワースペクトルに相当します。
制御工学の分野ではボード線図という道具を使うことがありますが、ボード線図のゲイン線図は振幅スペクトル、位相線図は位相スペクトルの情報に相当します。
図12：3つのスペクトル
付録：フーリエ係数の公式を理解する
A0（直流成分）の求め方
A0を求めることは簡単です。A0は直流成分、すなわちプラスにもマイナスにも触れない成分なので、1周期の波形のうち、プラスとマイナスに振れる分をキャンセルしてあげて、全体の平均値を求めればよいのです。
フーリエ級数に入力される関数は同じ形を繰り返す周期波形ですから、時刻0から始まり、周期Tまでの波形が繰り返されます。この0～Tの範囲を積分すると、波のプラスに触れた分とマイナスに振れた分がキャンセル（相殺）し、直流成分だけが残って足し合わされます。これを積分範囲の時間（T）で割ってあげれば、全体の平均値が求まります。
例えば図13のような波形x(t)を考えてみましょう。
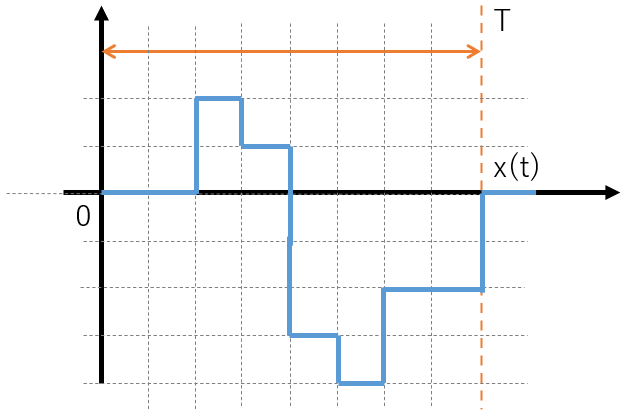
図13：周期波形から平均値を求める(1)
プラスに振れている部分（図14で黄色に塗った部分）はマイナスに振れている部分に同じ形がある（図14で薄緑に塗った部分）があるので、積分するとキャンセル（相殺）されます。
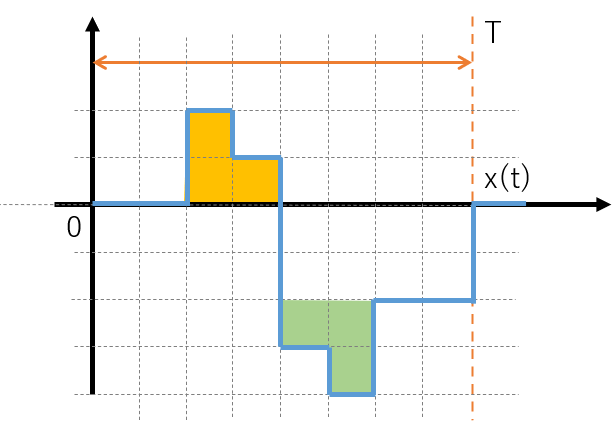
図14：周期波形から平均値を求める(2)
その結果、残った部分（図15でピンク色の部分）の面積が、積分の結果になります。数式で表すと
です。
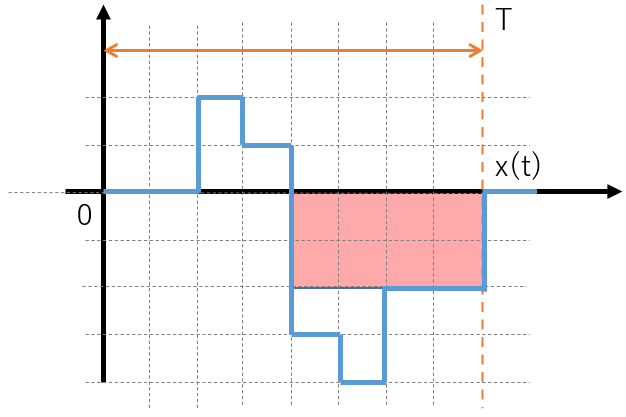
図15：周期波形から平均値を求める(3)
これを、波形の長さ（周期T）で割った値が、この波形の平均値です。数式で表すと
です。
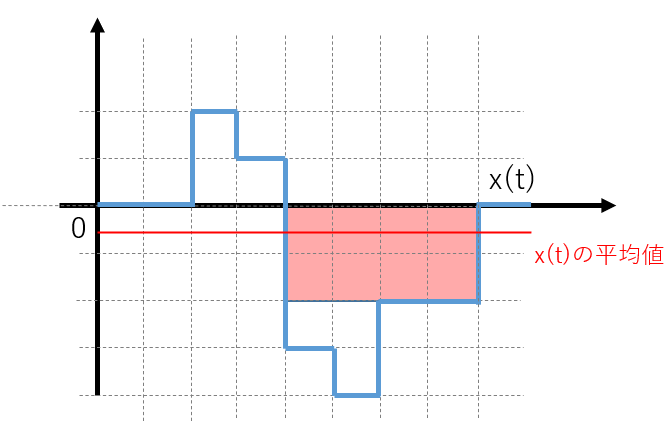
図16：周期波形から平均値を求める(4)
フーリエ係数A0を求める式は図17の通りです。x(t)の平均値を求める計算とほとんどいっしょであることがわかります。ただし他の式との整合性をとるため、平均値の「2倍」がA0の値になっています。
図17：フーリエ係数A0の式を読み解く
Ak（cosにかかる係数）とBk（sinにかかる係数）の求め方
AkとBkを求める式は、A0を求める式から考えると分かりやすいです。
先ほど説明した三角関数の直交性により、三角関数（sin, cos）同士の内積をとると、同じ三角関数かつ同じ周波数の信号成分だけが残り、他は0になります。この性質を利用することで、求めたい周波数だけを残して積分し、平均をとることで周波数成分の大きさを求めることができます。
図18に、フーリエ係数Ak, Bkを求める式を示します。
図18：フーリエ係数Ak, Bkの式を読み解く
もう少し数式を頑張れる人は、本当にこの式で求められるのか、確認してみましょう。
フーリエ係数Akを求める公式
を例にして考えます（Bkも全く同じ流れで確認できます）。
まず、周期Tを角周波数ωを使った表現に書き換えておきます。
なので
となります。そしてフーリエ級数展開は、元の関数x(t)を
の形で表現できるという主張でした。そこで、Akの公式にあるx(t)をフーリエ級数展開で置き換えてあげます（変数kが重複するので、混乱を避けるために変数は直します）。
これを展開します
さて、積分が3つも並んでしまいましたが、よく考えると1つ目の積分はcosを1周期にわたって積分しているだけです。これは計算するまでもなく0になることがわかります（cosは上下対称の波なので1周期積分すれば全てキャンセルされて0）。また、3つ目の積分はsinとcosの積なので、内積の定義からこれも0になります。結局残るのは2つ目の積分だけで、
Σが積分の内側にあるとわかりにくいので、Σと∫の順番を入れ替えましょう（このような入れ替えは常にできるわけではないので注意が必要です。この計算に関して言えば、Amは（積分にとっては）定数と考えられるので外にくくり出し、順序を入れ替えることが可能です）
内積の定義から、mω=kω、すなわちm=kの時に限りこの積分は値を持ち、他は0です。従って
この積分は手計算すると面倒ですので、ソフトウェアの力を借りましょう。Wolfram AlphaまたはMaximaで計算します。（図ではωの代わりにwと入れて計算しています）
図19：Wolfram Alphaを用いた積分計算
Maximaの場合は、wが正か負かと問われます。positiveと入力します。
図20：Maximaを用いた積分計算
いずれの場合も
という結果が得られます。ただし、kは整数という条件を考慮すると、sin(4πk)は常に0です。従って
という積分結果になります。結果を元の式に代入すると
目的のフーリエ係数だけが取り出されました！
こちらも是非
“もっと見る” ブログ
センサーのすべてがわかる！組み込み技術者のための基礎知識
私たちの生活を豊かにするために欠かせないセンサー。そんなセンサーの仕組みや種類について、分かりやすく解説していきます。
ブラシレスモーター制御用MCUをささっと動かしてみよう！【RL78編】
私の主観としては、”モーター制御用途でも十分使用可能な超汎用MCU”です。現状最も人に勧められるMCUの1つです。2つめのリンク stmcu.jpは、ログインする事でリファレンスマニュアルやペリフェラルの使い方に関する日本語資料が閲覧できますので、ユーザー登録をおススメします。
【フーリエ級数編2：世界で最も美しい数式】イメージでしっかりつかむ信号処理〜基礎から学ぶFFT〜
角度を表すとき、私たちは一般に円一周を360分割して単位[°]をつけた度数法を使用しています。数学の世界では度数法ではなく、弧度（こど）法という角度表現を用いることが一般的です。弧度法の単位は[rad]で、ラジアンまたはラディアンと読みます。円一周の角度を2π[rad]と定義する表現方法で、これは半径が１である円（単位円）をある角度で扇形に切り取ったとき、その中心角度を切り取った扇の外周の長さで表現する事に相当します。
