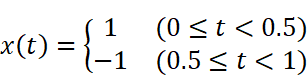本当にフーリエ級数で波形を再現できるのだろうか
ここまでフーリエ級数展開について説明をしてきましたが、本当にsinとcosの重ね合わせで波形を再現できるのだろうかと思っている方もいるかと思います。
そこで、代表的な3つの周期波形として「矩形波（方形波）」「ノコギリ波（鋸歯状波）」「三角波」をとりあげ、実際に波形を再現できることを確認してみましょう。
矩形波（方形波）の再現実験
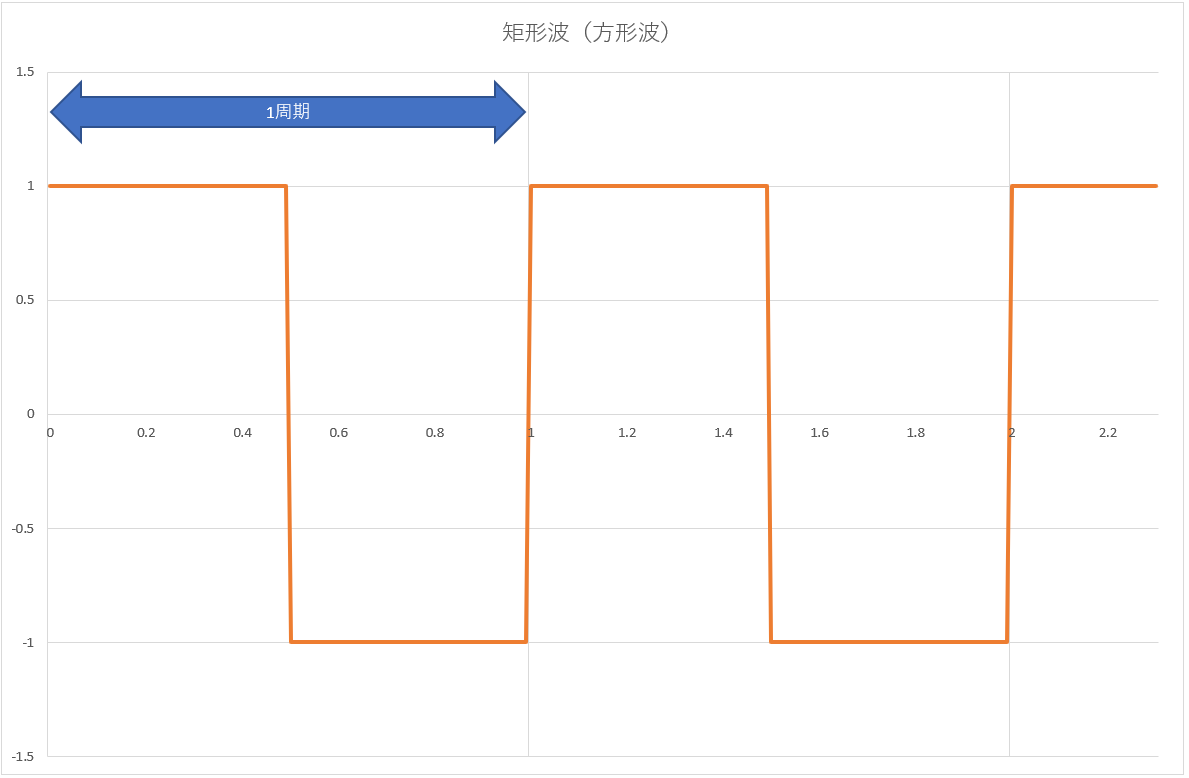
図1：矩形波（方形波）の例
波形の周期は１であり、最初の1周期を表す式は以下の通りです。
矩形波（方形波）のフーリエ係数を求める
A0を求める
A0を求める公式にx(t)と周期Ｔ=1を代入して計算します。この時、tの範囲を2つにわけて積分を作ることがポイントです。
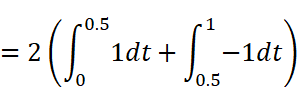
Wolfram AlphaまたはMaximaで計算します。
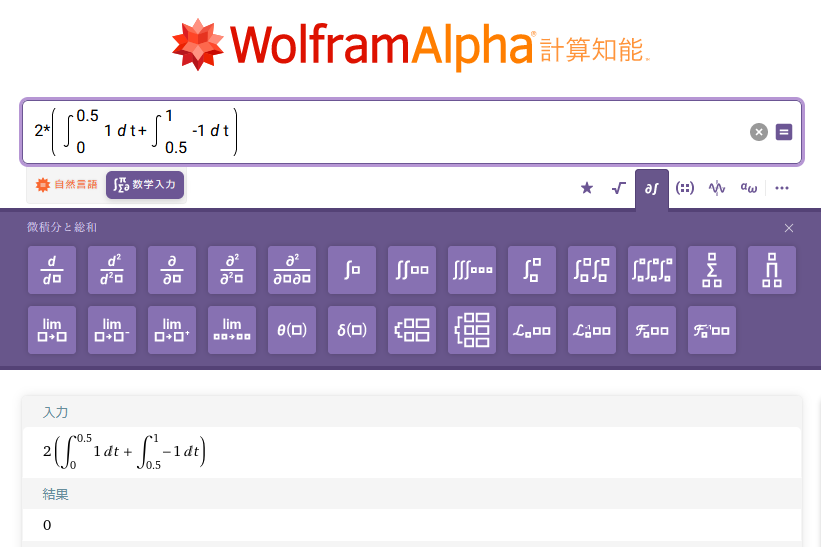
図2：Wolfram Alphaで矩形波（方形波）のA0を求める
図3：Maximaで矩形波（方形波）のA0を求める
従って、
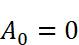
であることがわかります。
Akを求める
Akを求める公式にx(t)と周期Ｔ=1を代入して計算します。この時、tの範囲を2つにわけて積分を作ることがポイントです。
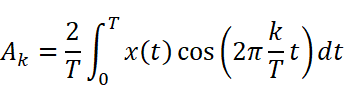
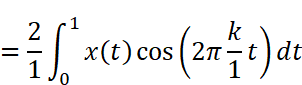
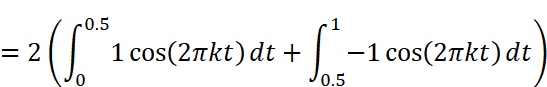
Wolfram AlphaまたはMaximaで計算します。なお、Wolfram Alphaで計算する時、積分範囲の0.5は分数表記（1/2）しないときれいな結果が出ませんでした。
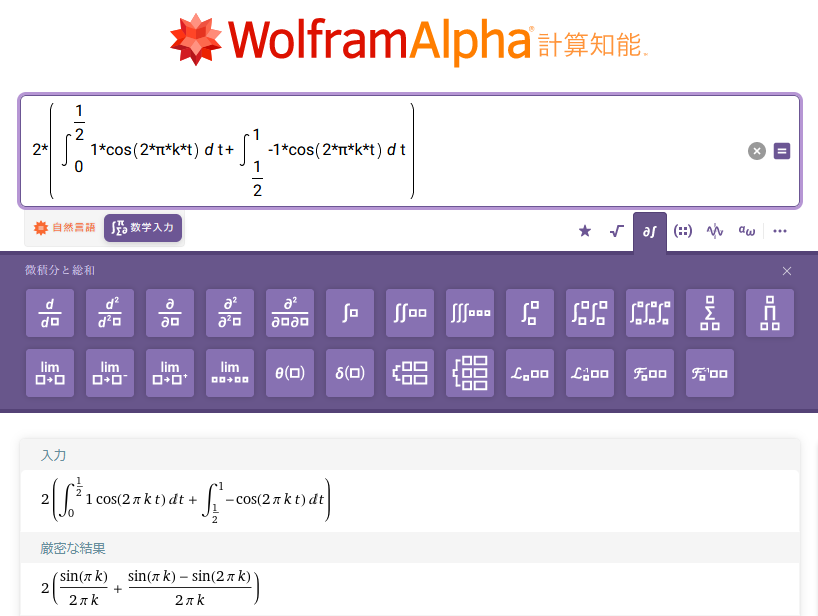
図4：Wolfram Alphaで矩形波（方形波）のAkを求める
図5：Maximaで矩形波（方形波）のAkを求める
Wolfram Alphaの出力とMaximaの出力は見た目がちょっと違いますが、どちらも同じ（等価な）計算結果を出しています。ただし、どちらの計算も「kが整数である」という事が考慮されていない事に注意が必要です。得られた計算結果
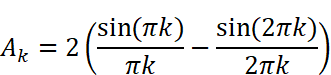
にはsin関数が2つ含まれています。kは整数（0,1,2…）なので、角度πkは0,π,2π,3π…とπ（180度）刻みで、角度2πkは0,2π,4π,6π…と2π（360度）刻みで変化することになります。しかし、sin(πk)=sin(0),sin(π),sin(2π)…は全て0になるので、結局
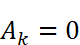
であることがわかります。
Bkを求める
Bkを求める公式にx(t)と周期Ｔ=1を代入して計算します。この時、tの範囲を2つにわけて積分を作ることがポイントです。
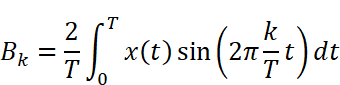
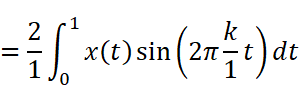
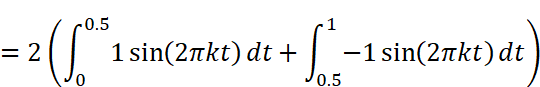
Wolfram AlphaまたはMaximaで計算します。なお、Wolfram Alphaで計算する時、積分範囲の0.5は分数表記（1/2）しないときれいな結果が出ませんでした。
図6：Wolfram Alphaで矩形波（方形波）のBkを求める
図7：Maximaで矩形波（方形波）のBkを求める
Wolfram Alphaの出力とMaximaの出力は見た目がちょっと違いますが、どちらも同じ（等価な）計算結果を出しています。ただし、どちらの計算も「kが整数である」という事が考慮されていない事に注意が必要です。得られた計算結果
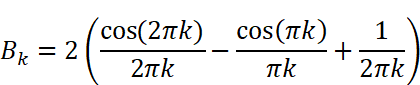
にはcos関数が2つ含まれています。kは整数（0,1,2…）なので、角度πkは0,π,2π,3π…とπ（180度）刻みで、角度2πkは0,2π,4π,6π…と2π（360度）刻みで変化することになります。cos(2πk )=cos(0),cos(2π),cos(4π) …は全て1ですが、cos(πk)はkが奇数の時-1、kが偶数の時に1となります。つまり
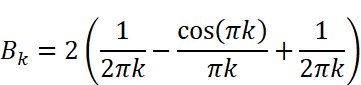
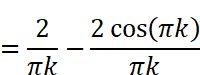
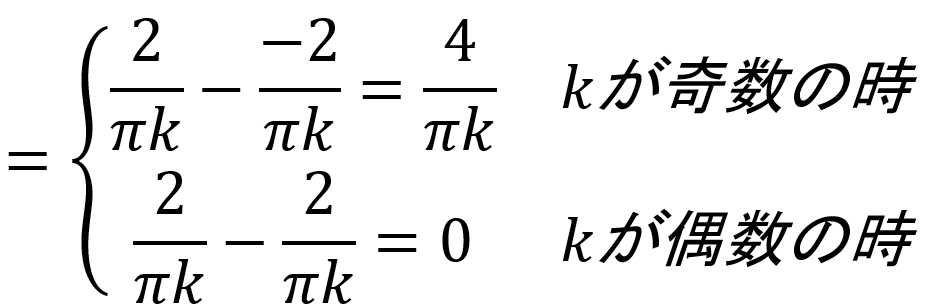
というように、kが奇数か偶数かで異なる値が得られます。
矩形波（方形波）のフーリエ係数
以上の計算を総合すると、矩形波（方形波）のフーリエ係数は以下のようになります。
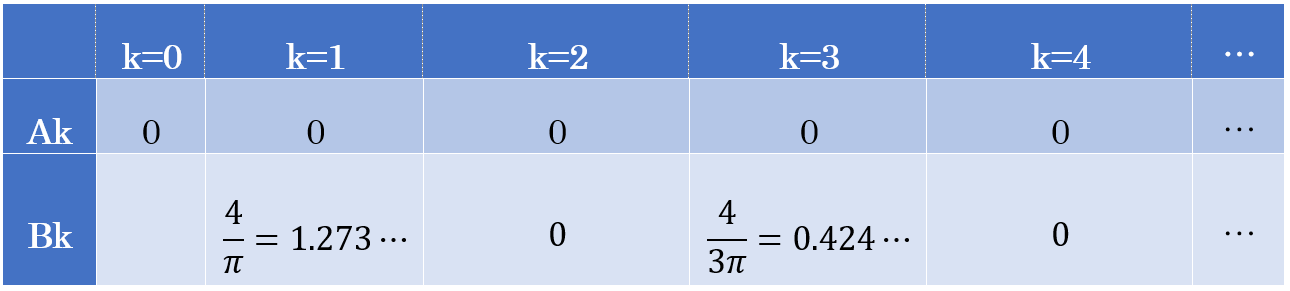
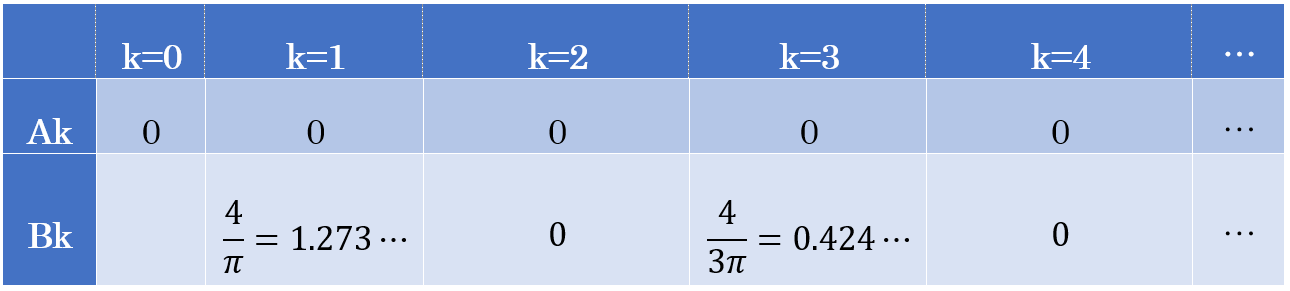
表1：矩形波（方形波）のフーリエ係数一覧
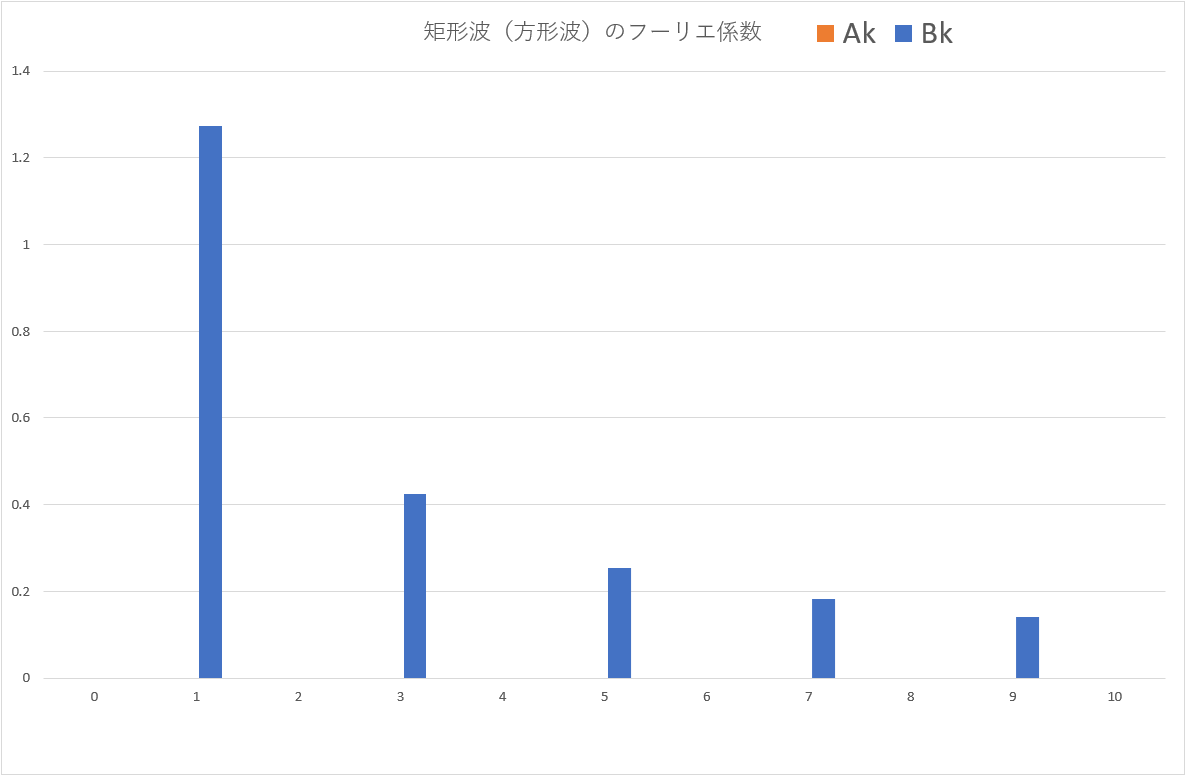
図8：矩形波（方形波）のフーリエ係数グラフ
矩形波（方形波）をフーリエ級数で再現する
求めたフーリエ係数で、矩形波（方形波）が再現できるのか、確認してみましょう。
フーリエ級数の式
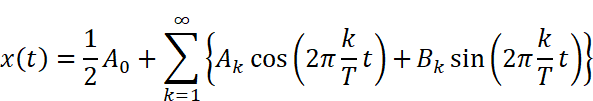
に、フーリエ係数及び周期T=1を代入します。無限の足し算を実際に行うことはできないので、総和の上限はひとまず10とおきます。
今回の場合A0とAkがゼロであるので
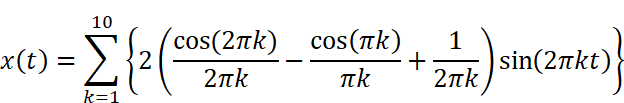
を計算し、グラフにしてみましょう。
Wolfram Alphaの場合は、上式をそのまま記入すると、グラフを描いてくれます。
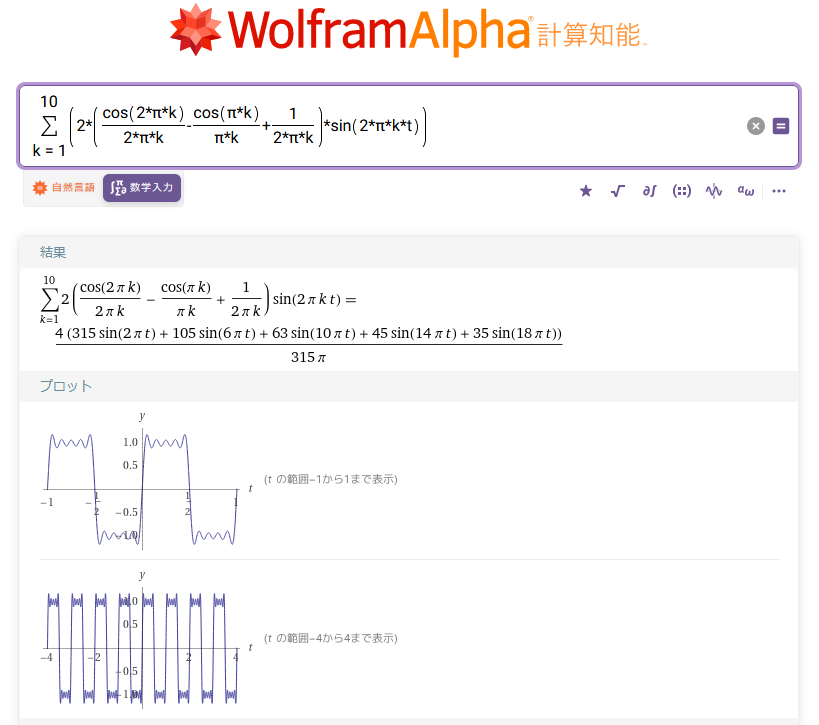
図9：Wolfram Alphaで矩形波（方形波）を再現
総和の上限が小さいのでかなり波打ってはいますが、矩形波（方形波）に近い形が得られていることがわかります。総和の上限をさらに大きくすればもっと近い形になるのですが、無料版のWolfram Alphaでは計算時間が長くなると強制的に処理を止められてしまうため、実験できません。
Maximaの場合は、まず関数B(k)とx(t)を定義した後、x(t)のグラフを描きます。
図10：Maximaで矩形波（方形波）を再現
次のようなグラフが得られます。
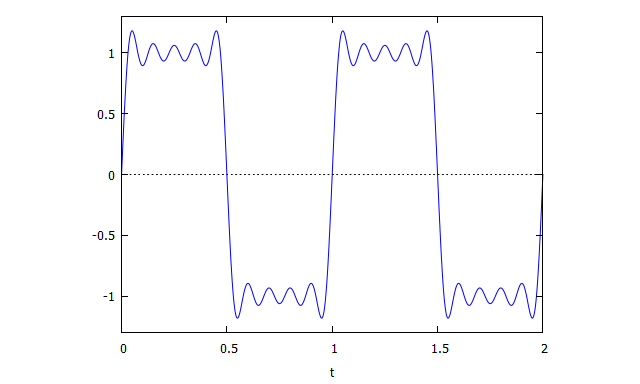
図11：Maximaで再現した矩形波（方形波）
Maximaであれば、総和の上限をさらに大きくすることが可能です。例えば総和の上限を500にするには、次のように入力します。
図12：Maximaでより精密な矩形波（方形波）を再現
ぐっと矩形波（方形波）に近づきました。
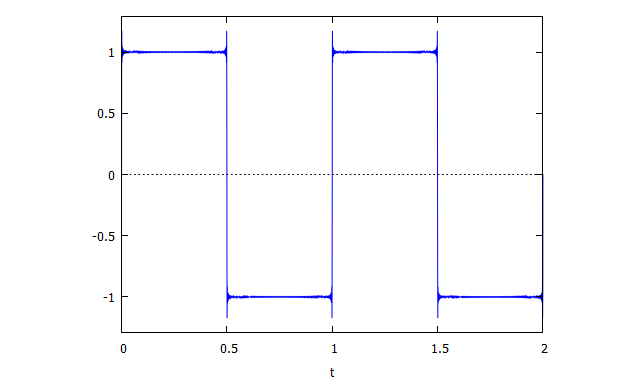
図13：Maximaで再現したより精密な矩形波（方形波）
ちょっと余談：ギブズの現象
矩形波を再現したフーリエ級数展開で、総和の数を500まで増やすと、出力はぐっと矩形波に近づきました。しかしよく見ると、波が跳躍する「カド」の部分にするどい「ヒゲ」が見えていることに気づきます。この「ヒゲ」を拡大してみると、「カド」の部分だけ波が振動的に増大していることがわかります。
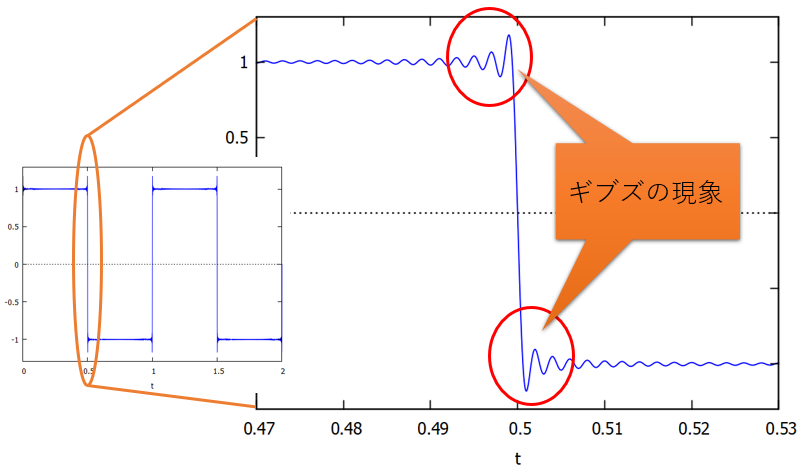
図14：ギブズの現象
この現象には「ギブズの現象」という名前がついています。矩形波の「カド」のように急激に変化する部分は、sin,cosのように滑らかな関数で再現することがとても難しい（数学的に表現するならば、「フーリエ級数の収束が非常に緩慢である」）ため、なかなか再現しきれないのです。とはいえ理論的には、無限に波を重ね合わせていくと究極的には再現できることになります。
ノコギリ波（鋸歯状波）の再現実験
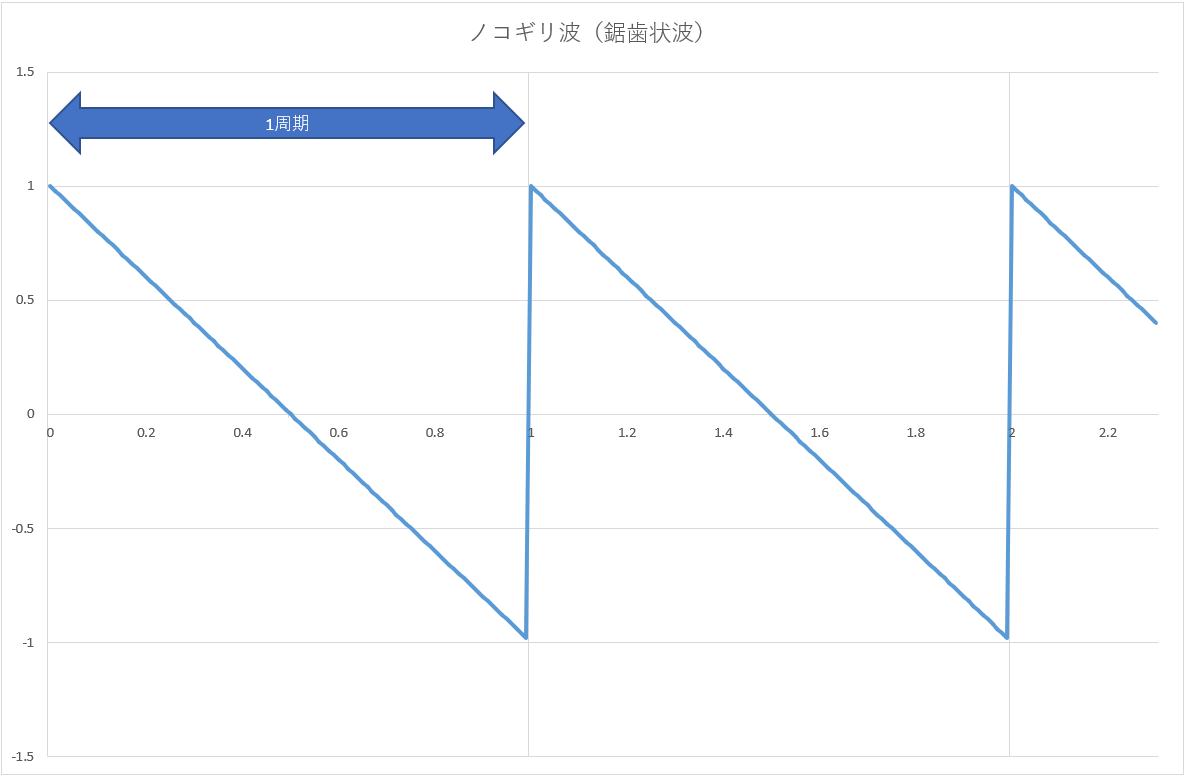
図15：ノコギリ波（鋸歯状波）の例
波形の周期は１であり、最初の1周期を表す式は以下の通りです。
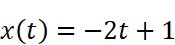
ノコギリ波（鋸歯状波）のフーリエ係数を求める
A0を求める
A0を求める公式にx(t)と周期Ｔ=1を代入して計算します。
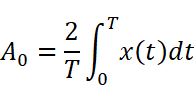
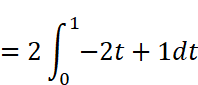
Wolfram AlphaまたはMaximaで計算します。
図16：Wolfram Alphaでノコギリ波（鋸歯状波）のA0を求める
図17：Maximaでノコギリ波（鋸歯状波）のA0を求める
従って、
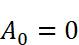
であることがわかります。
Akを求める
Akを求める公式にx(t)と周期Ｔ=1を代入して計算します。
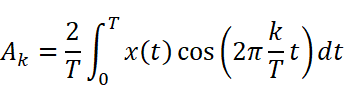
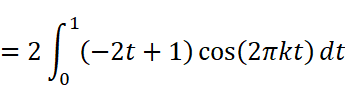
Wolfram AlphaまたはMaximaで計算します。
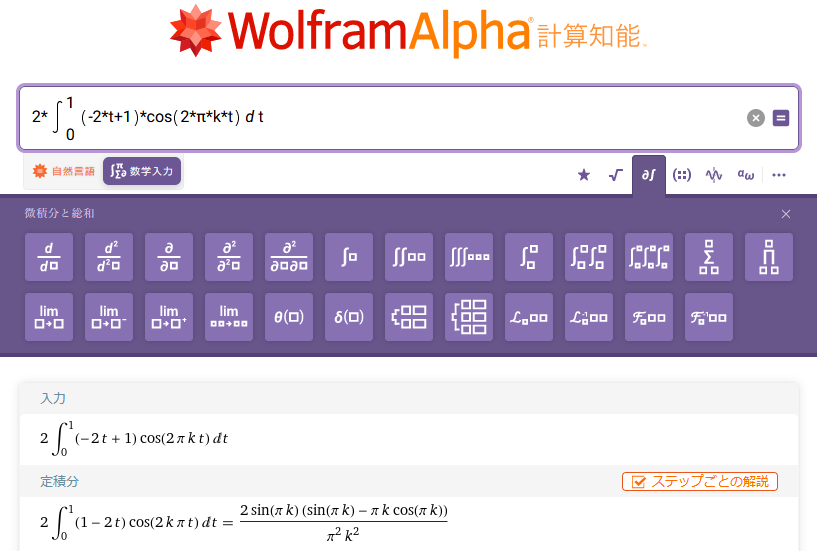
図18：Wolfram Alphaでノコギリ波（鋸歯状波）のAkを求める
図19：Maximaでノコギリ波（鋸歯状波）のAkを求める
Wolfram Alphaの出力とMaximaの出力は見た目がちょっと違いますが、どちらも同じ（等価な）計算結果を出しています。ただし、どちらの計算も「kが整数である」という事が考慮されていない事に注意が必要です。得られた計算結果
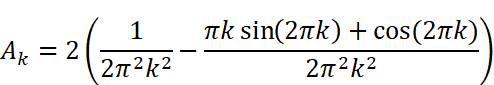
にはsin関数とcos関数が含まれています。kは整数（0,1,2…）なので、角度2πkは0,2π,4π,6π…と2π（360度）刻みで変化することになります。しかし、sin(2πk )=sin(0),sin(2π),sin(4π)…は全て0、 cos(2πk )=cos(0),cos(2π),cos(4π) …は全て1です。従って
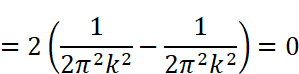
すなわち、
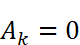
であることがわかります。
Bkを求める
Bkを求める公式にx(t)と周期Ｔ=1を代入して計算します。
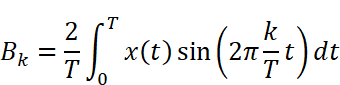
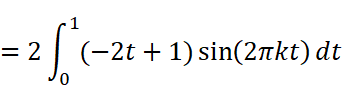
Wolfram AlphaまたはMaximaで計算します。
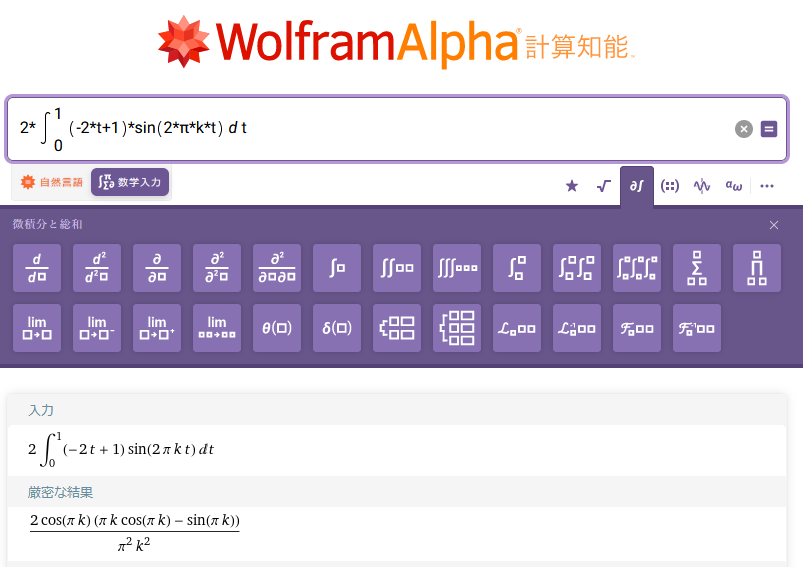
図20：Wolfram Alphaでノコギリ波（鋸歯状波）のBkを求める
図21：Maximaでノコギリ波（鋸歯状波）のBkを求める
Wolfram Alphaの出力とMaximaの出力は見た目がちょっと違いますが、どちらも同じ（等価な）計算結果を出しています。ただし、どちらの計算も「kが整数である」という事が考慮されていない事に注意が必要です。得られた計算結果
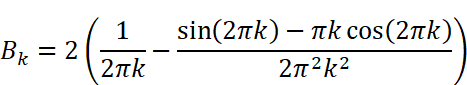
にはsin関数とcos関数が含まれています。kは整数（0,1,2…）なので、角度2πkは0,2π,4π,6π…と2π（360度）刻みで変化することになります。しかし、sin(2πk )=sin(0),sin(2π),sin(4π)…は全て0、 cos(2πk )=cos(0),cos(2π),cos(4π) …は全て1です。従って
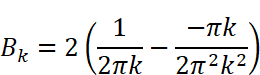
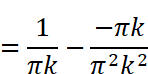
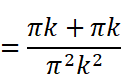
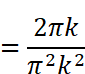
という値が得られます。
ノコギリ波（鋸歯状波）のフーリエ係数
以上の計算を総合すると、矩形波（方形波）のフーリエ係数は以下のようになります。
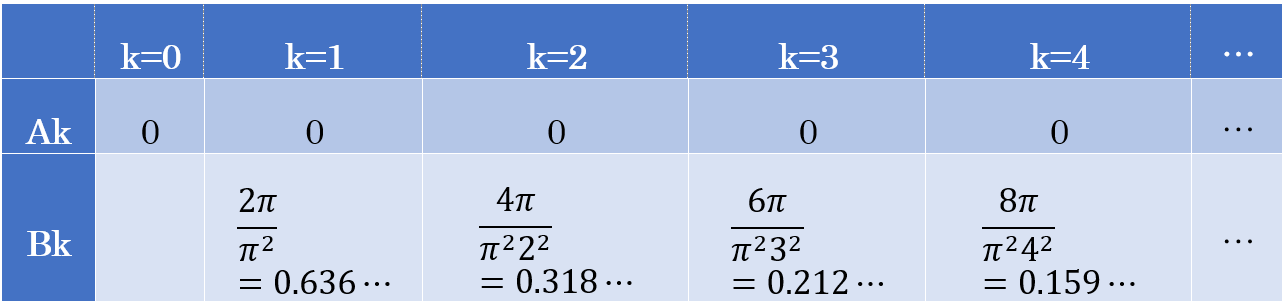
表2：ノコギリ波（鋸歯状波）のフーリエ係数一覧
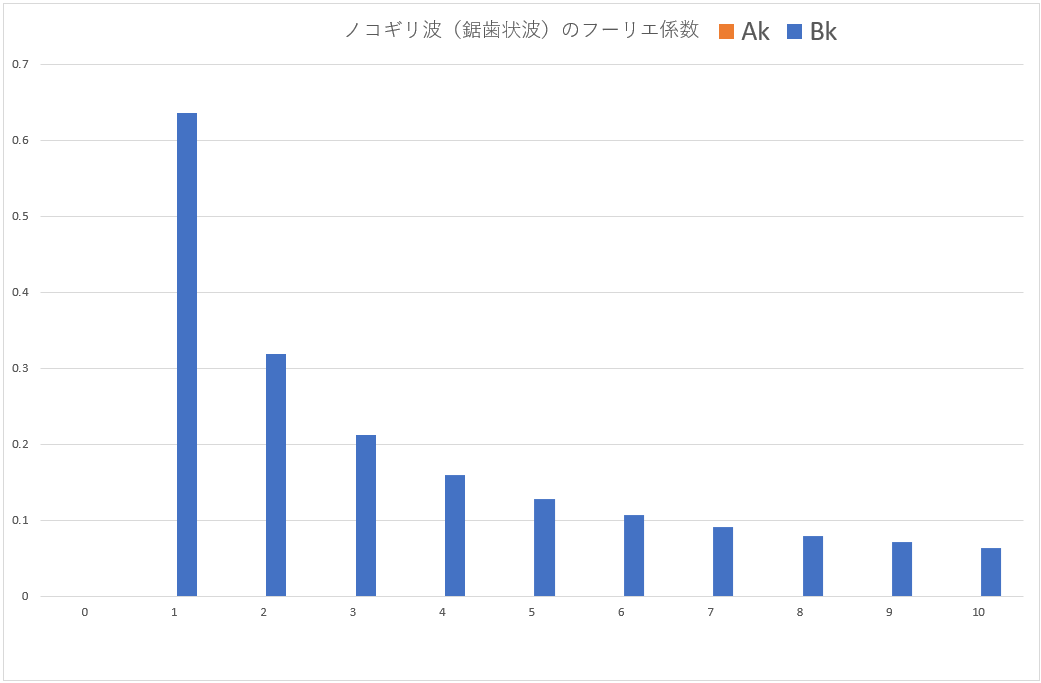
図22：ノコギリ波（鋸歯状波）のフーリエ係数グラフ
ノコギリ波（鋸歯状波）をフーリエ級数で再現する
求めたフーリエ係数で、ノコギリ波（鋸歯状波）が再現できるのか、確認してみましょう。
フーリエ級数の式
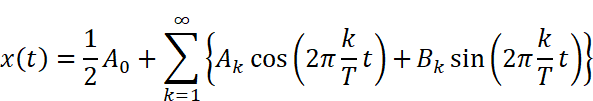
に、フーリエ係数及び周期T=1を代入します。無限の足し算を実際に行うことはできないので、総和の上限はひとまず10とおきます。
今回の場合A0とAkがゼロであるので
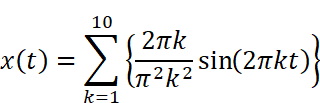
を計算し、グラフにしてみましょう。
Wolfram Alphaの場合は、上式をそのまま記入すると、グラフを描いてくれます。
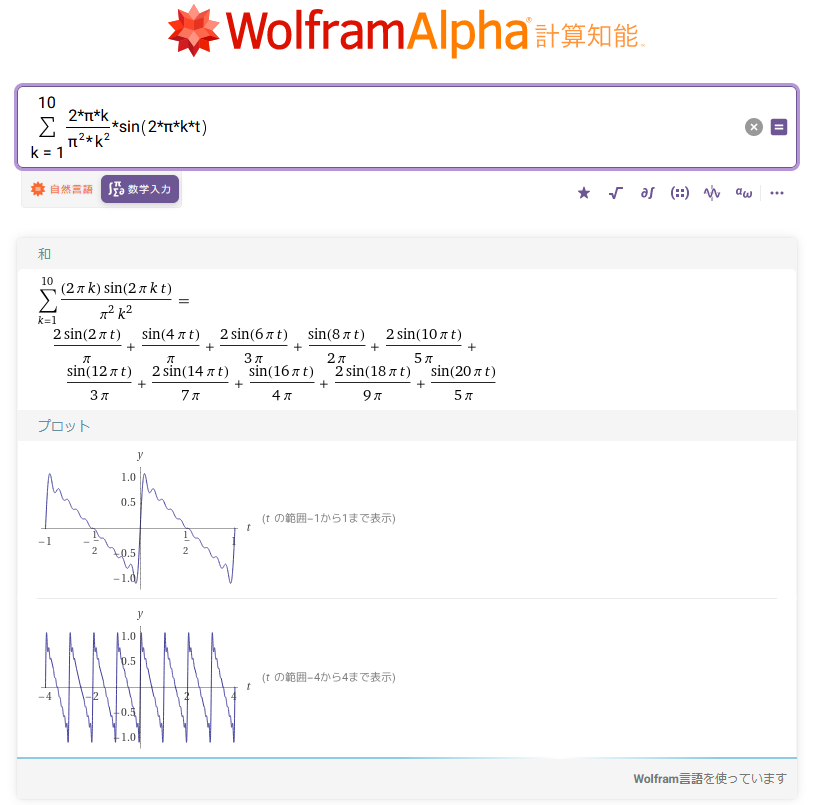
図23：Wolfram Alphaでノコギリ波（鋸歯状波）を再現
総和の上限が小さいのでかなり波打ってはいますが、ノコギリ波（鋸歯状波）に近い形が得られていることがわかります。総和の上限をさらに大きくすればもっと近い形になるのですが、無料版のWolfram Alphaでは計算時間が長くなると強制的に処理を止められてしまうため、実験できません。
Maximaの場合は、まず関数B(k)とx(t)を定義した後、x(t)のグラフを描きます。
図24：Maximaでノコギリ波（鋸歯状波）を再現
次のようなグラフが得られます。
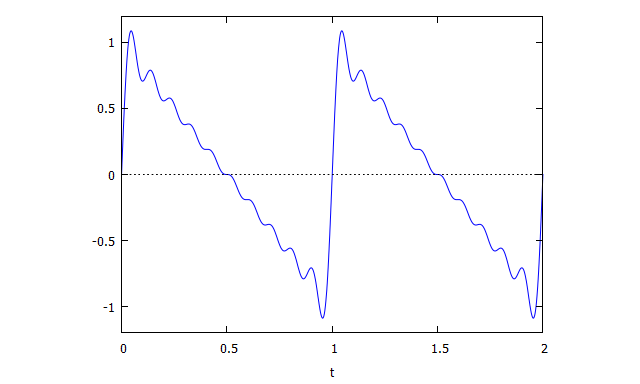
図25：Maximaで再現したノコギリ波（鋸歯状波）
Maximaであれば、総和の上限をさらに大きくすることが可能です。例えば総和の上限を500にするには、次のように入力します。
図26：Maximaでより精密なノコギリ波（鋸歯状波）を再現
ぐっとノコギリ波（鋸歯状波）に近づきました。
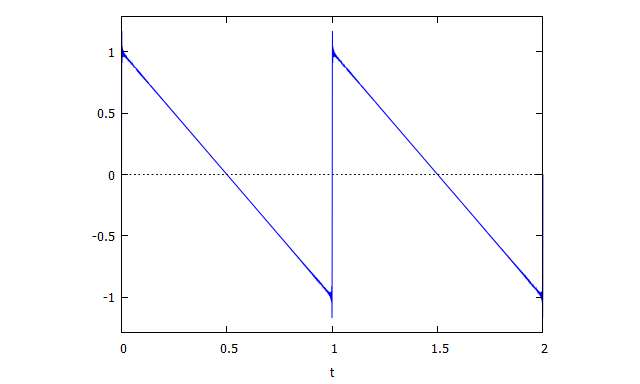
図27：Maximaで再現したより精密なノコギリ波（鋸歯状波）
ちょっと余談：係数Akが0になる関数
関数には「奇関数」と呼ばれるものがあり、以下の関係式を満たす関数を指します。
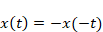
別の言い方をすれば、「関数のグラフを描いた時、原点を中心に点対称の波形になる関数」という事もできます。本稿で扱った「ノコギリ波」はこれに当てはまります。奇関数には「フーリエ級数展開すると、係数Akが0になる」という特徴があります。
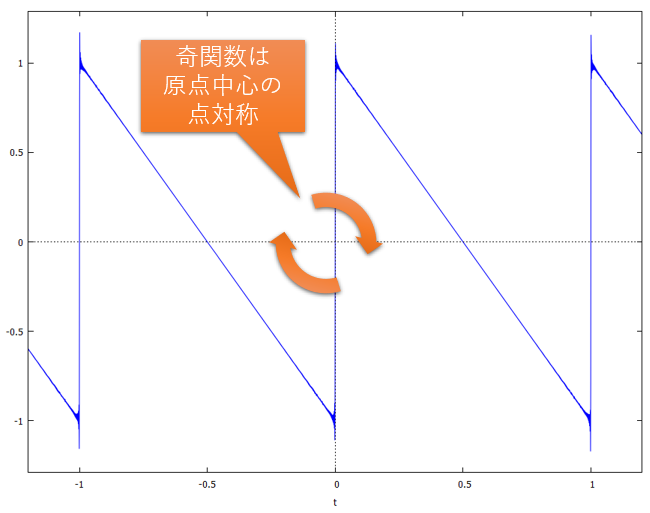
図28：奇関数
三角波の再現実験
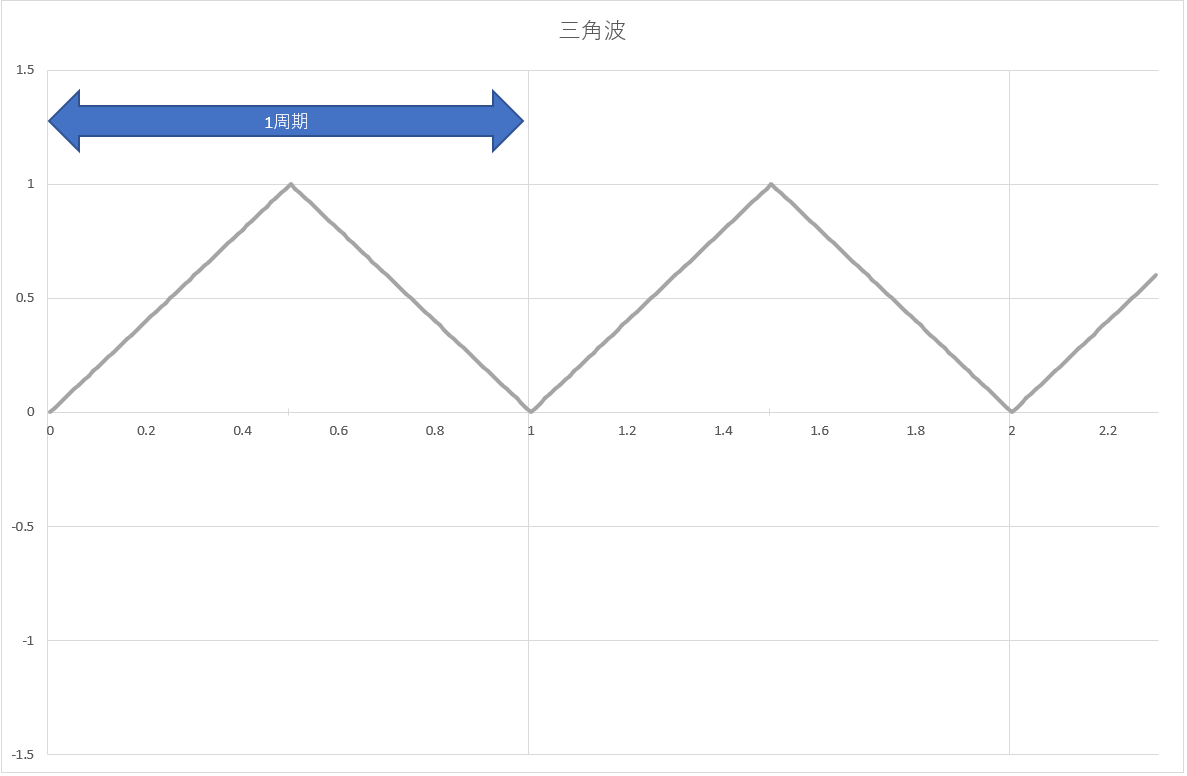
図29：三角波の例
波形の周期は１であり、最初の1周期を表す式は以下の通りです。
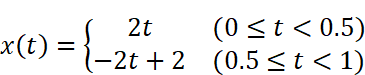
三角波のフーリエ係数を求める
A0を求める
A0を求める公式にx(t)と周期Ｔ=1を代入して計算します。この時、tの範囲を2つにわけて積分を作ることがポイントです。
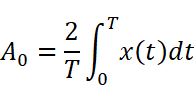
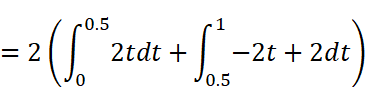
Wolfram AlphaまたはMaximaで計算します。
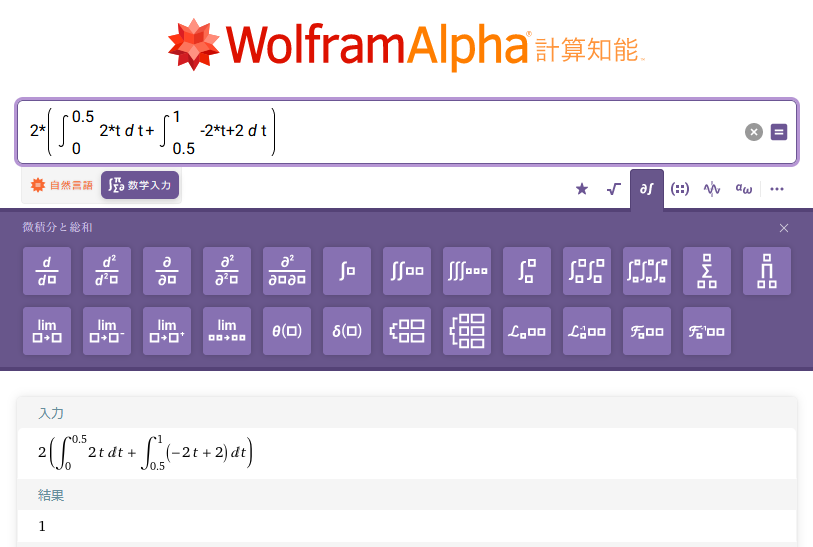
図30：Wolfram Alphaで三角波のA0を求める
図31：Maximaで三角波のA0を求める
従って、
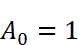
であることがわかります。
Akを求める
Akを求める公式にx(t)と周期Ｔ=1を代入して計算します。この時、tの範囲を2つにわけて積分を作ることがポイントです。
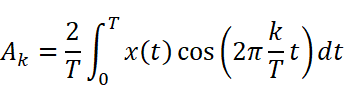
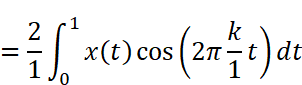
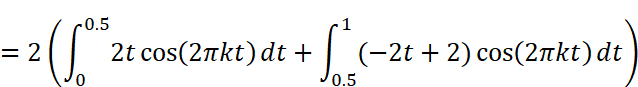
Wolfram AlphaまたはMaximaで計算します。なお、Wolfram Alphaで計算する時、積分範囲の0.5は分数表記（1/2）しないときれいな結果が出ませんでした。
図32：Wolfram Alphaで三角波のAkを求める
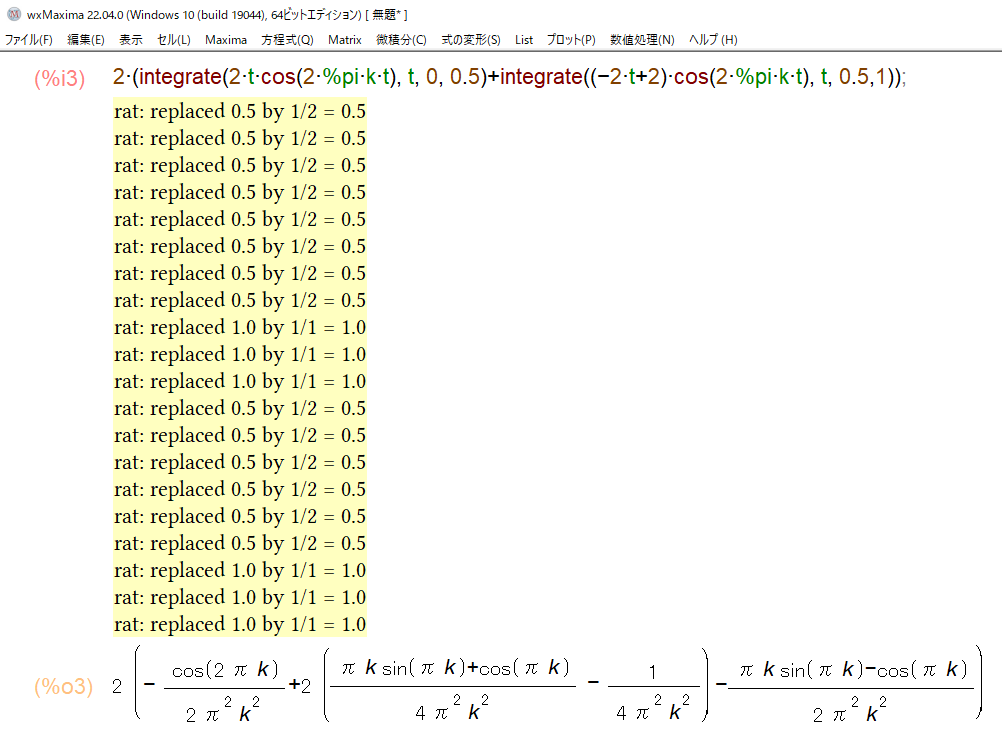
図33：Maximaで三角波のAkを求める
Wolfram Alphaの出力とMaximaの出力は見た目がちょっと違いますが、どちらも同じ（等価な）計算結果を出しています。ただし、どちらの計算も「kが整数である」という事が考慮されていない事に注意が必要です。得られた計算結果
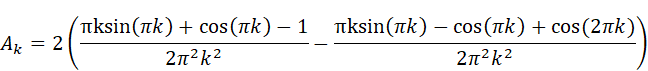
にはsin関数とcos関数が含まれています。kは整数（0,1,2…）なので、角度πkは0,π,2π,3π…とπ（180度）刻みで、角度2πkは0,2π,4π,6π…と2π（360度）刻みで変化することになります。しかし、sin(πk)=sin(0),sin(π),sin(2π)…は全て0であり、cos(2πk )=cos(0),cos(2π),cos(4π) …は全て1です。cos(πk)はkが奇数の時-1、kが偶数の時に1となります。つまり
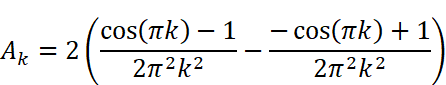
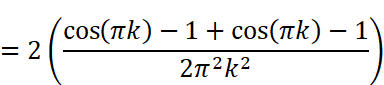
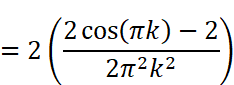
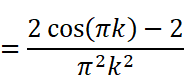
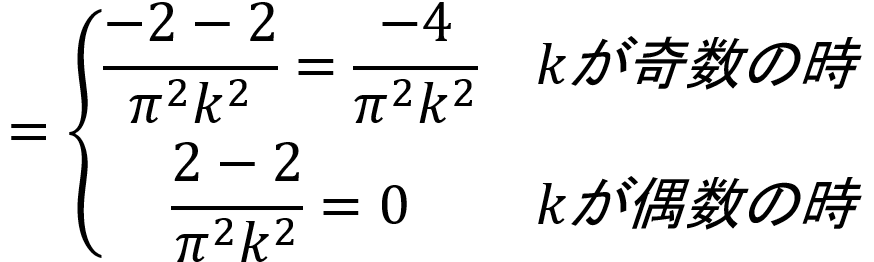
というように、kが奇数か偶数かで異なる値が得られます。
Bkを求める
Bkを求める公式にx(t)と周期Ｔ=1を代入して計算します。この時、tの範囲を2つにわけて積分を作ることがポイントです。
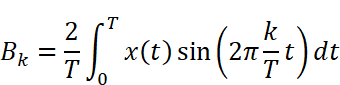
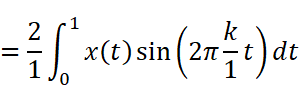
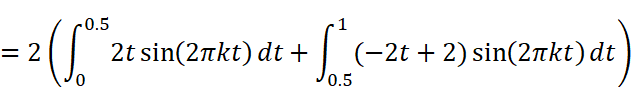
Wolfram AlphaまたはMaximaで計算します。なお、Wolfram Alphaで計算する時、積分範囲の0.5は分数表記（1/2）しないときれいな結果が出ませんでした。
図34：Wolfram Alphaで三角波のBkを求める
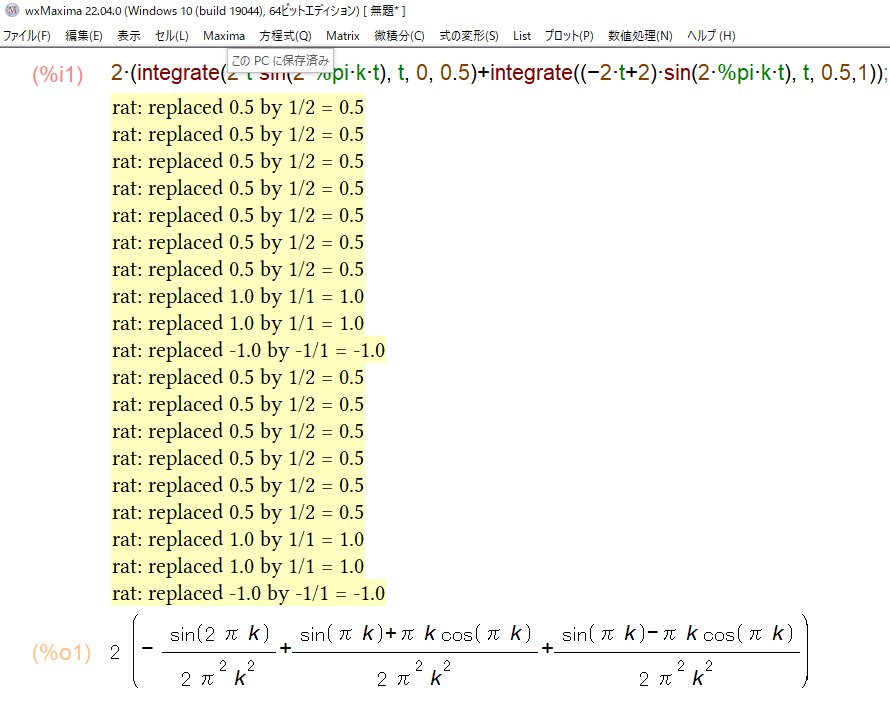
図35：Maximaで三角波のBkを求める
Wolfram Alphaの出力とMaximaの出力は見た目がちょっと違いますが、どちらも同じ（等価な）計算結果を出しています。ただし、どちらの計算も「kが整数である」という事が考慮されていない事に注意が必要です。得られた計算結果
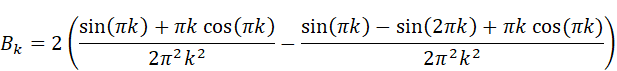
にはsin関数とcos関数が含まれています。kは整数（0,1,2…）なので、角度πkは0,π,2π,3π…とπ（180度）刻みで、角度2πkは0,2π,4π,6π…と2π（360度）刻みで変化することになります。しかし、sin(πk)=sin(0),sin(π),sin(2π)…及びsin(2πk )=sin(0),sin(2π),sin(4π) …は全て0です。つまり
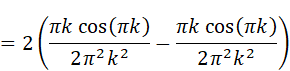
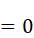
結局
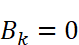
であることがわかります。
三角波のフーリエ係数
以上の計算を総合すると、三角波のフーリエ係数は以下のようになります。
表3：三角波のフーリエ係数一覧
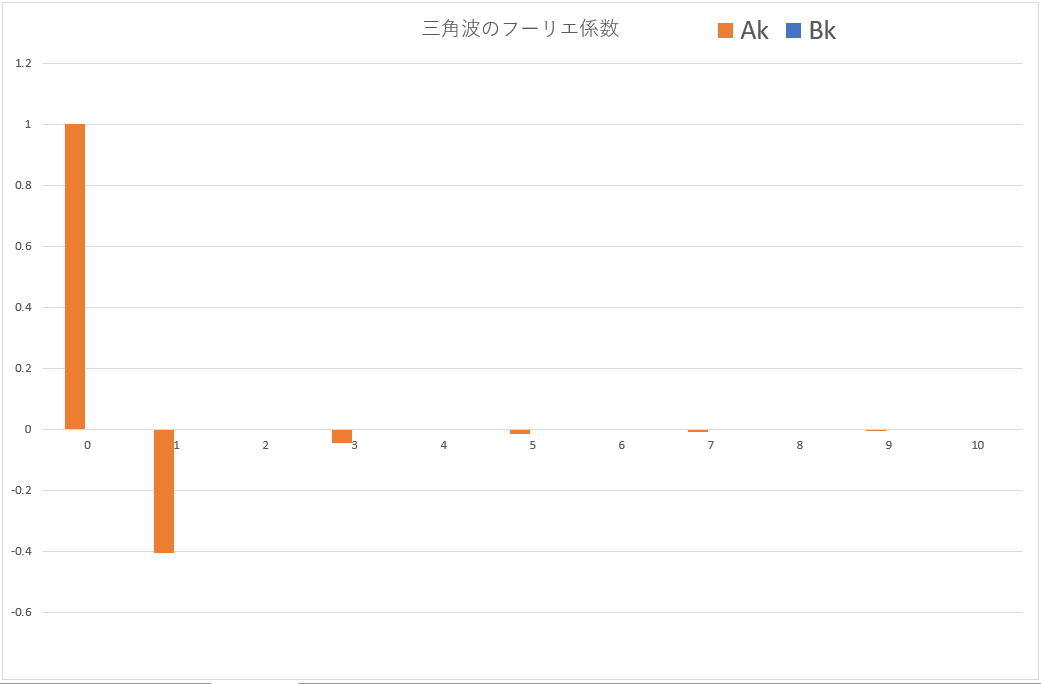
図36：三角波のフーリエ係数グラフ
三角波をフーリエ級数で再現する
求めたフーリエ係数で、三角波が再現できるのか、確認してみましょう。
フーリエ級数の式
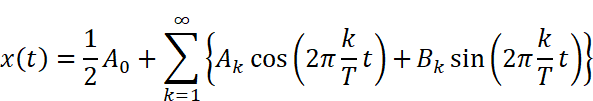
に、フーリエ係数及び周期T=1を代入します。無限の足し算を実際に行うことはできないので、総和の上限はひとまず10とおきます。
今回の場合Bkがゼロであるので
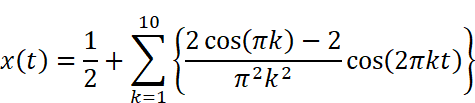
を計算し、グラフにしてみましょう。
Wolfram Alphaの場合は、上式をそのまま記入すると、グラフを描いてくれます。
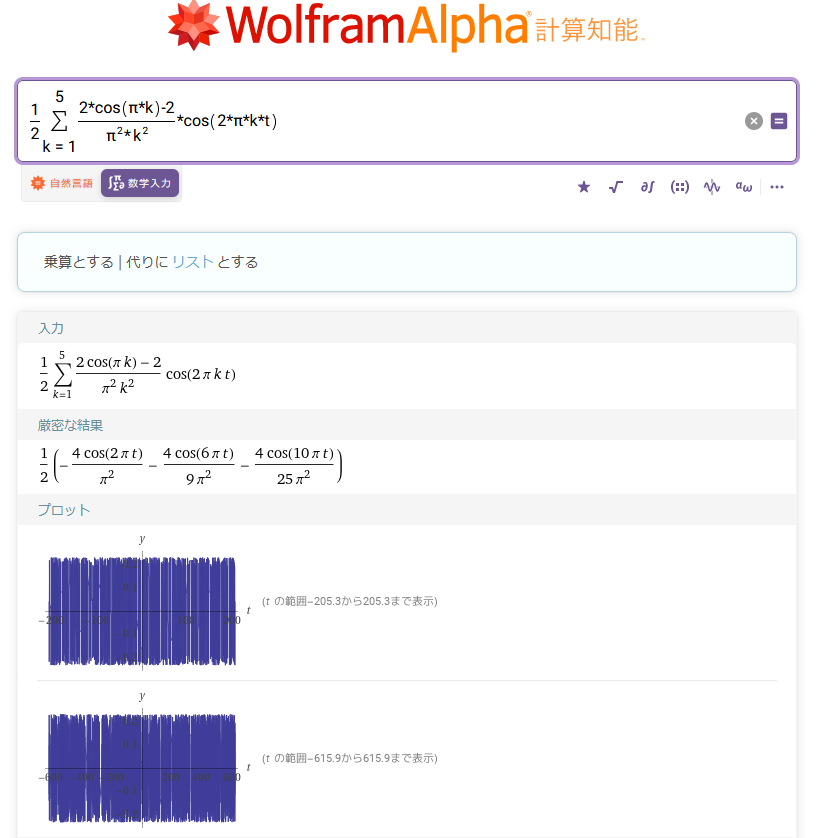
図37：Wolfram Alphaで三角波を再現
描いてはくれているのですが、tの範囲がとても広いため、波形がよく見えません（有料アカウントを持っていればグラフの拡大表示ができます）。しかしコマンドを以下のようにちょっと一工夫すると、拡大できます。
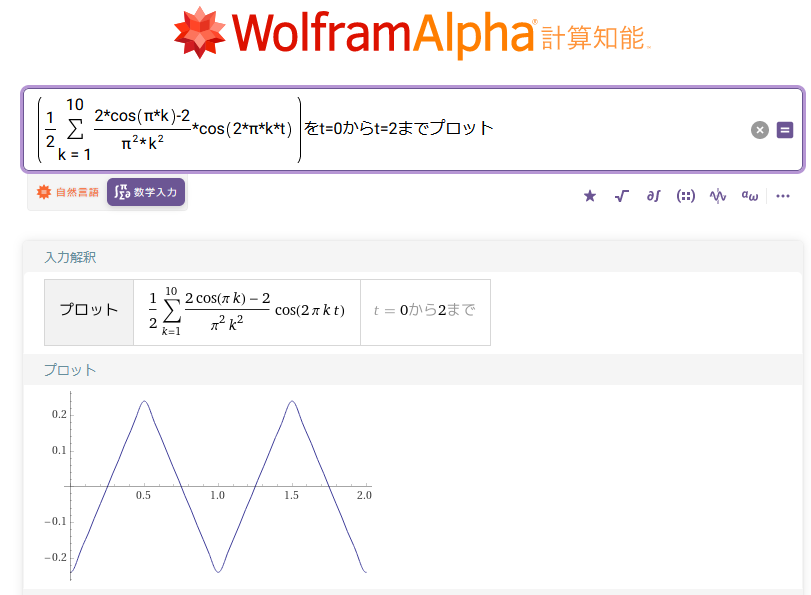
図38：Wolfram Alphaで三角波を再現（拡大表示）
総和の上限が小さいので角が少し丸まっていますが、三角波に近い形が得られていることがわかります。総和の上限をさらに大きくすればもっと近い形になるのですが、無料版のWolfram Alphaでは計算時間が長くなると強制的に処理を止められてしまうため、実験できません。
Maximaの場合は、まず関数A(k)とx(t)を定義した後、x(t)のグラフを描きます。
図39：Maximaで三角波を再現
次のようなグラフが得られます。
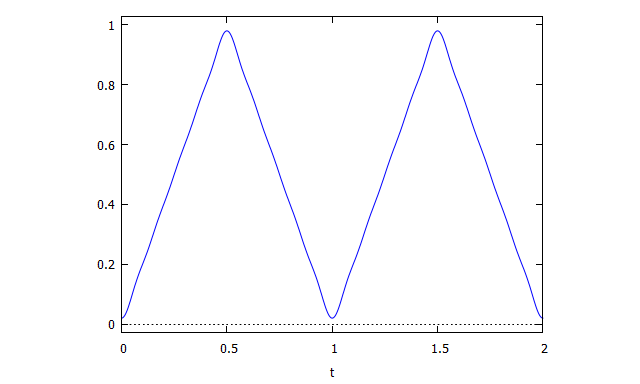
図40：Maximaで再現した三角波
Maximaであれば、総和の上限をさらに大きくすることが可能です。例えば総和の上限を500にするには、次のように入力します。
図41：Maximaでより精密な三角波を再現
ぐっと三角波に近づきました。
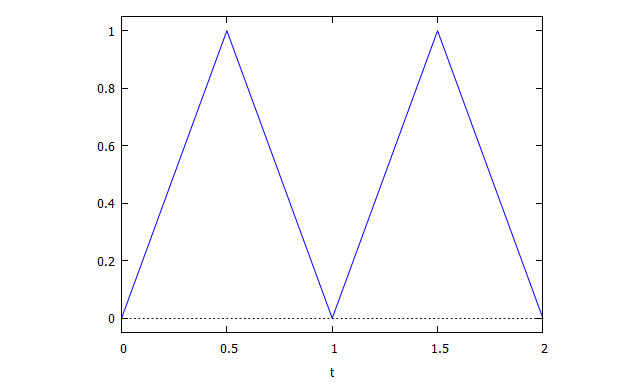
図42：Maximaで再現したより精密な三角波
ここまでで、フーリエ級数編は終わりです。次回からはフーリエ級数を「フーリエ変換」に発展させていきます。
ちょっと余談：係数Bkが0になる関数
関数には「偶関数」と呼ばれるものがあり、以下の関係式を満たす関数を指します。
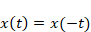
別の言い方をすれば、「関数のグラフを描いた時、y軸を中心に線対称の波形になる関数」という事もできます。本稿で扱った「三角波」はこれに当てはまります。偶関数には「フーリエ級数展開すると、係数Bkが0になる」という特徴があります。
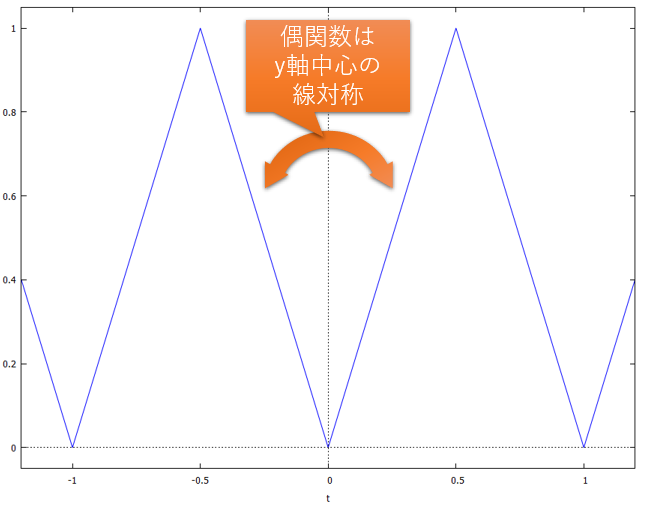
図43：偶関数
こちらも是非
“もっと見る” ブログ
センサーのすべてがわかる！組み込み技術者のための基礎知識
私たちの生活を豊かにするために欠かせないセンサー。そんなセンサーの仕組みや種類について、分かりやすく解説していきます。
ブラシレスモーター制御用MCUをささっと動かしてみよう！【RL78編】
私の主観としては、”モーター制御用途でも十分使用可能な超汎用MCU”です。現状最も人に勧められるMCUの1つです。2つめのリンク stmcu.jpは、ログインする事でリファレンスマニュアルやペリフェラルの使い方に関する日本語資料が閲覧できますので、ユーザー登録をおススメします。
【フーリエ級数編2：世界で最も美しい数式】イメージでしっかりつかむ信号処理〜基礎から学ぶFFT〜
角度を表すとき、私たちは一般に円一周を360分割して単位[°]をつけた度数法を使用しています。数学の世界では度数法ではなく、弧度（こど）法という角度表現を用いることが一般的です。弧度法の単位は[rad]で、ラジアンまたはラディアンと読みます。円一周の角度を2π[rad]と定義する表現方法で、これは半径が１である円（単位円）をある角度で扇形に切り取ったとき、その中心角度を切り取った扇の外周の長さで表現する事に相当します。
