はじめに
この連載の最終目標
私たちのまわりには、たくさんの「信号」があふれています。人間だけでなく、コンピュータもまたたくさんの「信号」を受け取ったり、送ったりして動作しています。その「信号」が常にキレイで、間違いなく、わかりやすく伝わってくれれば楽なのですが…実際の信号にはノイズという汚れが混じり、読み取り間違いを起こすことも多く、そしてわかりにくい(直接内容を読み取れない)形で伝わる事が多々ある、やっかいな存在でもあります。
このやっかいな「信号」をうまく扱うためのノウハウが集まっているのが「信号処理」と呼ばれる学問分野です。この連載では、信号処理の基本にして重要なツールである「フーリエ級数展開とその仲間」について学び、最後は「FFT(高速フーリエ変換)」まで理解することを最終目標とします。以下。フーリエ級数展開とその仲間・FFTを合わせて「フーリエ分析」と呼ぶことにします。
信号処理は数学の応用分野ですので、どうしても数式(数学)から逃れることはできません。しかしできるだけ余計な寄り道をしないで、最短ルートを精選して話を進めていきます。その分、必要最低限の数式をできるだけ丁寧に。そして数式が示す「イメージ」をつかめるように解説していきたいと思います。
参考書
この連載で解説する「フーリエ分析」というのは、同じ内容を説明しているにもかかわらず、細かな定義の仕方によって数式表現が大きく変わります。そのため、数式に慣れていない人は複数の本や資料を突き合せたときに混乱してしまいます。
この連載で使用する数式表現は、基本的に高橋信『 テキスト入門 信号処理のための数学』(オーム社)に合わせています。読みやすく、説明も丁寧な良書ですので、本連載をさらに深く理解するための参考書が必要な人は本書を併せて手元に置いておくことをお勧めします。
そもそも「信号」「信号処理」とは何?
「信号」とは
「皆さんの身の周りにある「信号」と名のつくものを挙げて下さい」と言われて、どんなものを思い出すでしょうか。
最も身近なものは、道路に設置されている、自動車や歩行者用の信号機でしょう。鉄道ファンであれば、鉄道用の信号を思い出した人もいるかもしれません。またミリタリーファンであれば、船同士の通信で使用する手旗信号や、かつて無線通信で使用していたモールス信号を思い出した人もいるでしょう。これ以外にも、私たちの身の周りには数多くの「信号」が存在しています。
「信号」を簡単に説明すると、のろし(煙)、時報(音)、手旗信号(手の動き)など、音・光・色・動き・形などを通じて「何かしらの意味を伝送すること」ということができます。信号と名前がついていなくても、何らかの意味を伝送する仕組みが整っていれば、それは「信号」として扱うことができます。
「信号処理」とは
信号処理(Signal Processing)は文字通り、信号に対して何らかの「処理」を行う技術を集めた学問分野です。信号処理は大きく分けると、信号を新たに作り出す「信号生成」と、ノイズに埋もれた情報や、人間が理解できない信号から情報を取り出す「信号解析」の2つに分類できます。
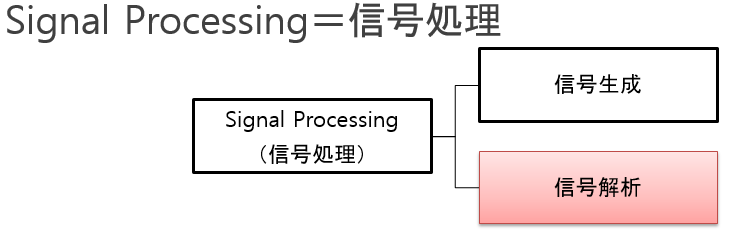
図1:信号処理
この連載で学ぶ内容は、後者の「信号解析」にあたります。特に基本となる1次元のデータ(ほとんど場合時系列データ)の分析方法を学びます。具体例としては、直観的にわかりやすい音声信号を主に取り扱います。
フーリエ分析とスペクトル
では、フーリエ分析ができると、何が嬉しいのでしょう。
皆さんは太陽や電球の光を三角柱状のレンズ(プリズム)に通して、虹を作る実験を行った事があるでしょうか。

図2:プリズムによる分光実験
これはプリズムに白色光(太陽光)を入力したことで、光の波長(周波数)別に成分が分離される、分光という現象によって起こります。プリズムから出た虹は、赤から紫まで、波長の短い順(周波数の低い順)に色が並んだものです。このように、元の信号からその周波数成分を取り出して順番に並べたものを「スペクトル」といいます。
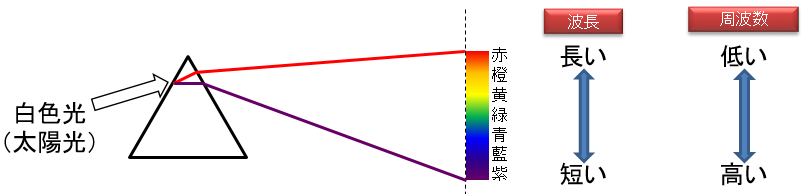
図3:分光の仕組みとスペクトル
本連載で学ぶ「フーリエ分析」は、まさに信号のスペクトログラム、すなわち入力信号を「周波数別に分解したもの」を求める手法になります。音の信号をフーリエ分析すると、エフェクタとして音に加工を掛けたり、混じってしまったノイズだけを除去したり、音声分析(音声入力・話者識別…)を行うなど、幅広い応用が可能になります。
いざ、信号処理の世界へ!
それではいざ、信号処理の世界へ足を踏み入れましょう。まずはフーリエ分析を理解するために、あらかじめ備えておきたい基礎知識をおさらいします。多少の数式がどうしても出てきてしまいますが、恐れないで下さい。大切なのは数式を丸覚えすることより、まずはその数式が表す「イメージ」を読み解く想像力です。一緒に学んでいきましょう。
こちらも是非
“もっと見る” ブログ
はじめての耐量子暗号
量子コンピューティングはさまざまな面で明るい未来のために期待される技術である反面、その演算能力をセキュリティ上の攻撃に使われることを考えると、既存の暗号技術にとって深刻な脅威でもあります。
Arm®対応のWindows IoT OS 【Windows IoT on Arm】を評価ボードで動かしてみる
組み込み機器向けOS、Windows 10/11 IoT Enterprise(以下Windows IoT)がサポートするArmプラットフォームが拡大しています。Windows IoT on Armは、Windows IoTのメリットそのまま、より低コストで低消費電力というArmならではのメリットもございます
【フーリエ級数からフーリエ変換へ:フーリエ変換編1】イメージでしっかりつかむ信号処理〜基礎から学ぶFFT〜
ここまで学んできたフーリエ級数展開は、「入力信号が周期波形でなければならない」という制約がありました。上図のような太鼓の音、すなわち単発波形は、フーリエ級数展開できないのでしょうか














