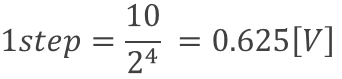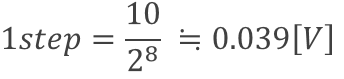アナログ信号とデジタル信号
信号処理で扱う信号は「アナログ信号」と「デジタル信号」の2つに大きく分けることができます。
私たちの身の周りにある物理量はほとんど全て「アナログ(Analog)信号」と言えます。アナログ信号の特徴は「連続信号」、すなわち信号に切れ目がなく、無限に細かい分割ができることが特徴です。アナログ信号の長所は物理的な上限制約はどうしてもありますが、その上限範囲のなかでは無限に細かい情報を表現できることです。その一方でアナログ信号の短所はノイズの影響を受けやすく、保存/コピー/伝送することでどうしても劣化してしまうこと、そしてノイズが入ったり劣化したりしてしまうと、それを完全に復元することができないというところが欠点です。

図1:アナログ信号の特徴
一方、コンピュータが扱う信号は全てデジタル(Digital)信号です。デジタル信号の特徴は「離散信号」、すなわち信号に切れ目があって飛び飛びで、数えられる(分割に上限がある)ことが特徴です。デジタル信号の長所と短所は、ほぼアナログ信号の真逆となります。デジタル信号の長所はノイズの影響を受けにくく、情報理論(前回記事参照)の技術によってエラー訂正も可能である事です。そして何より、コンピュータによる計算処理と相性が良い事が長所です。逆に短所としては、信号の表現精度に限界がある事です。

図2:デジタル信号の特徴
信号の表現精度については、絵で考えるとわかりやすいです。まず、なめらかに変化するアナログ信号を用意して、横軸(時間軸)と縦軸(信号強度)に一定間隔の目盛線を引きます。
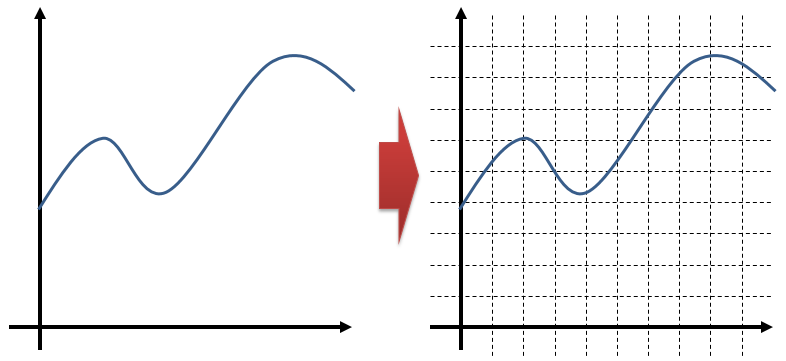
図3:アナログ信号の縦横軸に目盛線を引く
アナログ信号をデジタル信号にするということは、この目盛線が交差する「格子点」に信号の値を近似する事です。格子点の間を直線でつなぐと、デジタル信号に変わります。
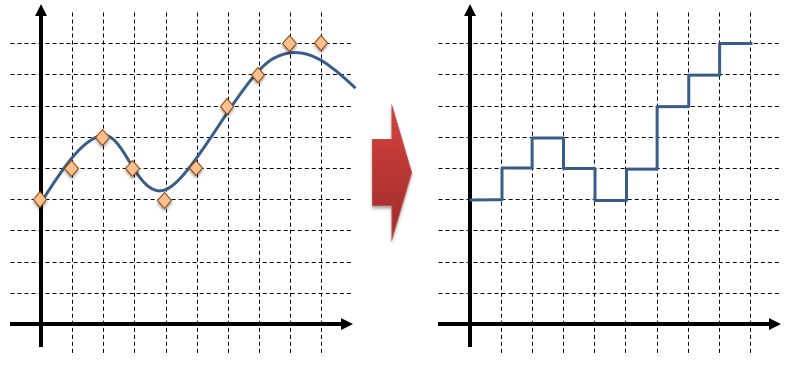
図4:格子点をつないでデジタル信号にする
目盛線の間隔が十分に小さい(細かい格子になる)場合は、アナログ信号とデジタル信号は似た形状になりますが、目盛線の間隔が大きい(粗い格子になる)場合は両者の違いが著しくなる事が想像できるでしょう。
A/D変換
A/D変換
先述のように、アナログ信号をデジタル信号に変換することをA/D変換(エーディー変換:Analog to Digital変換)と言います。私たちの身の周りにある信号は基本的にアナログ信号ですから、これをコンピュータ(マイコン)に取り込むためには必ずA/D変換を行う必要があります。
A/D変換は、「標本化」「量子化」「符号化」という3つのステップで成り立っています。

図5:A./D変換の手順
標本化(時間の離散化)
アナログ信号の時系列を一定間隔ごとに抽出する処理(時間の離散化)を「標本化」または「サンプリング」といいます。標本化の時間間隔は一般に周波数の形で表し、これを「標本化周波数」「サンプリング周波数」といいます。
周波数というのは、「1秒あたりの回数」で、単位は[Hz](ヘルツ)で表します。サンプリング周波数の場合、例えば1秒間に5000回の抽出をするならば、サンプリング周波数は5[kHz](=5000Hz)ということになります。また周波数と周期(間隔)は互いに逆数の関係にあります。サンプリング周波数が5000Hzであれば、サンプリング周期(サンプリング間隔)は1/5000=0.0002[sec]=0.2[msec]です。
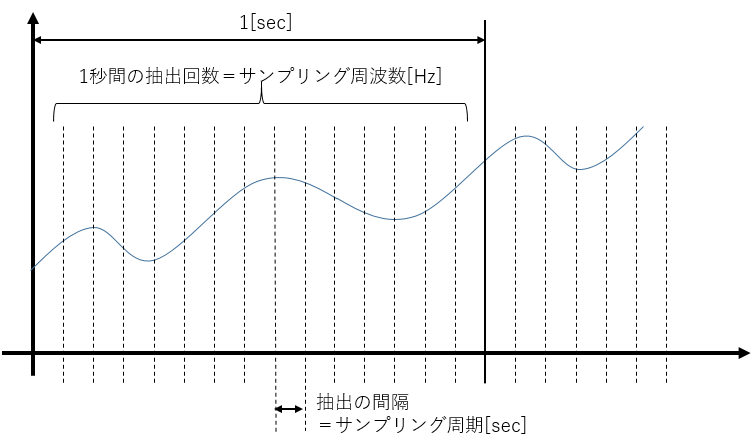
図6:サンプリング周波数とサンプリング周期の関係
A/D変換において、サンプリング周波数をいくつに設定するかはとても重要なことです。なぜならば、サンプリング周波数を高くする時と低くするとき、それぞれに表に示すようなメリット・デメリットがあって、両立することはできないからです。

表1:サンプリング周波数のメリットとデメリット
では、いったいどうやって周波数を決めればいいのでしょうか。
標本化(サンプリング)定理
サンプリング周波数を決めるために考慮すべき大事な法則が「標本化(サンプリング)定理」です。サンプリング周波数と信号の再現度の関係を定量的に表した関係式になります。

図7:標本化(サンプリング)定理…基本的な表現
どうしてこのような式になるかと言うと、図のように、最低限正弦波の山・谷の頂点をサンプリングする事さえできれば、残りの部分は数式で補間することができるためです。1周期(繰り返し波形の1単位)のうち、山・谷の2点をサンプリングすることになるのでサンプリング周波数は元の波形(の最大周波数)の2倍になるわけですね。これよりもサンプリング周波数が低くなってしまうと、信号の正しい再現は物理的に不可能となります。
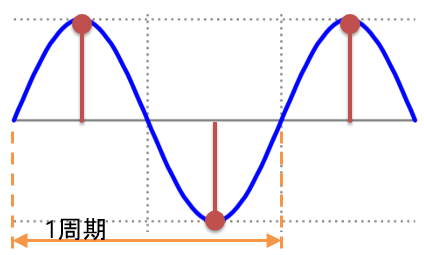
図8:正弦波の山谷の頂点が決まれば、残りは補間できる
「標本化(サンプリング)定理」は信号の最大周波数を基準にした時に、必要最低限なサンプリング周波数を定義する式になっていましたが、を逆にサンプリング周波数を基準として、表現できる上限周波数を定義する式で表すこともできます。この上限周波数は「ナイキスト周波数」といいます。

図9:標本化(サンプリング)定理…ナイキスト周波数を用いた表現
ちょっと余談:音楽CDのサンプリング周波数はなぜ44.1[kHz]?
人間の耳が聞き取れる周波数の範囲(可聴周波数)は20[Hz]~20[kHz]とされています。最大周波数20[kHz]を標本化後も再現するためには、標本化定理からサンプリング周波数2×20=40[kHz]が必要になります。
これに10%のマージン(余裕)をもたせると40×1.1=44[kHz]です。
この44[kHz]に近いサンプリング周波数として44.1[kHz]が選ばれたのは、ディジタルオーディオ信号をVTR(ビデオテープレコーダ)に記録する規格が作られた際、VTRの規格に合わせたサンプリング周波数として、選ばれたことにはじまります。
量子化(振幅の離散化)
標本化によって時間の離散化を行った後、量子化によって振幅方向も離散化します。振幅の間隔を一定間隔にとる場合(線形量子化)と、異なる間隔にする場合(非線形量子化)の両方がありますが、ここでは一番基本である線形量子化のみ考えます。
量子化も標本化と同様、離散化の間隔が細かいほど元信号の再現率が高くなります。振幅離散化の細かさは、最小~最大値までの分割数を2進数何ビットで表現できるかで表し、この値を「量子化ビット数」といいます。また(入力の)アナログ電圧と(出力の)デジタル信号が正しく対応づけられる最大電圧をフルスケール(FS)電圧といいます。例えば、フルスケール電圧が10[Vp-p](p-pはPeak to Peakのこと、すなわち波形の最大値と最小値の差を意味します)である信号を量子化ビット数4ビットで量子化すると、1ステップ当たりの電圧は以下のように計算できます。
この時、入力と出力の関係は次のようになります。
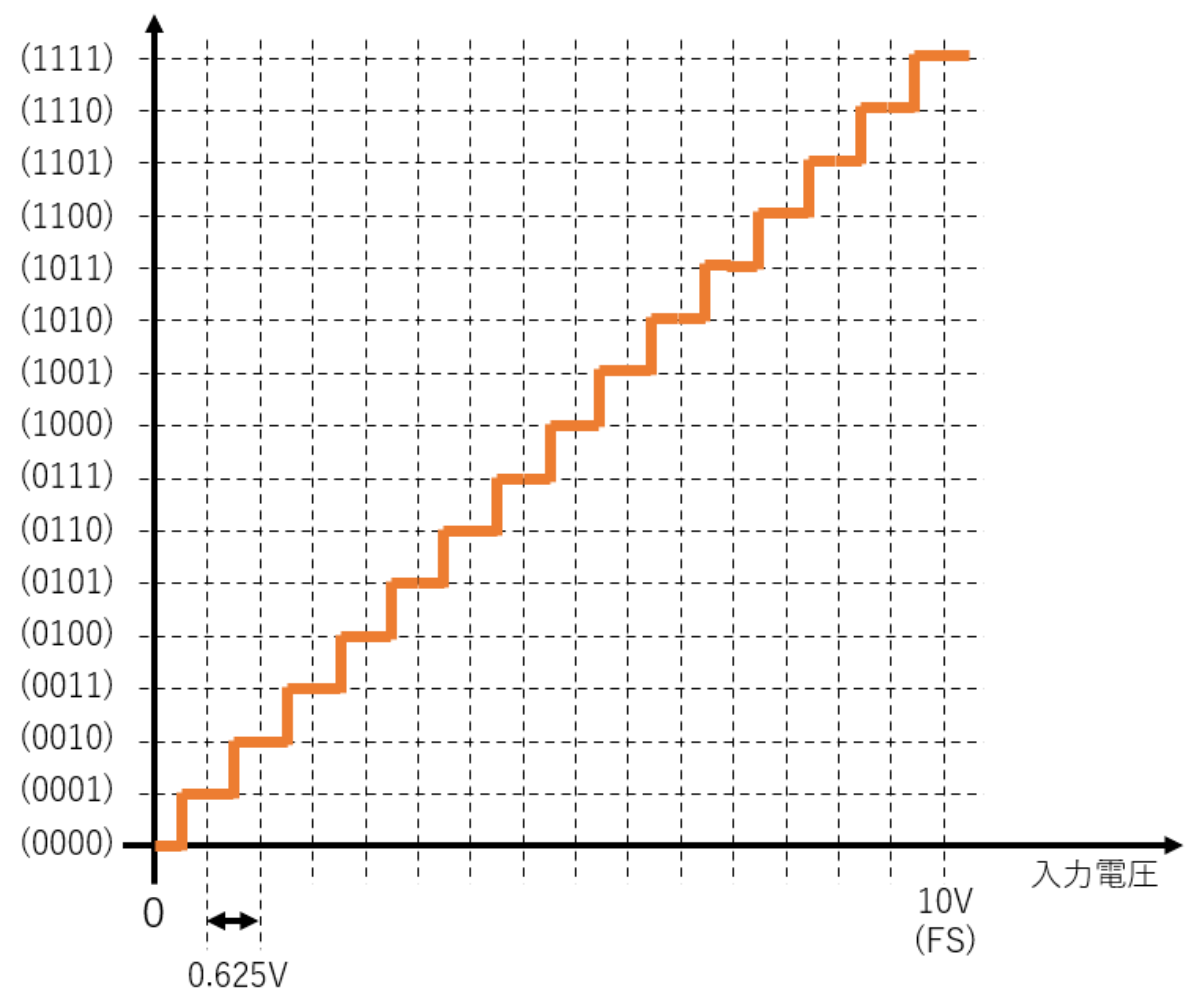
図10:4ビットで量子化した時の入力電圧と出力信号の関係
同様に、フルスケール電圧が10[Vp-p]である信号を量子化ビット数8ビットで量子化すると、1ステップ当たりの電圧は以下のように計算できます。
量子化ビット数と(最大値から最小値までの)分割数は、図のように2のべき乗と(2を底にした)対数の関係にあります。
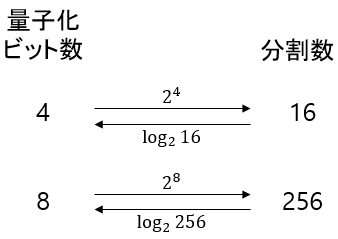
図11:量子化ビット数と分割数の関係
量子化によって、信号の形は(変換前の)真の値から、むりやり近似値に丸められてしまいます。これにより生じる誤差を「量子化誤差」と言います。丸められることで元信号にあったノイズが消えることがある、という話は先にしましたが、逆に量子化によって階段状の、角のある波形が生まれるため、新たなノイズ(量子化ノイズ)を生んでしまう欠点もあります。
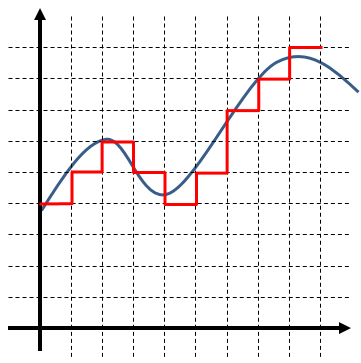
図12:アナログ信号とデジタル信号の比較
符号化(標本化・量子化後の値をデジタルデータに直す)
符号化は、標本化と量子化を終えた信号を0/1のデータに変換する作業です。音のような1次元信号であれば、標本化・量子化した値を時系列順にひたすら並べるのが最も単純な方法で、このような方法をPCM(Pulse Code Modulation)と言います。
実際のデータフォーマットの規格では「ヘッダ情報をどう入れるか」「情報の符号をどう表現するか(補数表現?ゲタ上げ?)」「パリティ(エラー訂正符号)の有無は?種類は?」など、もっと細かいさまざまなルールが定められます。たとえば音声信号のフォーマットであるWave形式は、基本的には単純なPCMデータですが、PCMデータと共にチャンネル数やサンプリング周波数などの情報も一緒に保存します。データサイズが大きくなるのが欠点です。以下の図はあるWaveファイルを、中身を直接表示してくれるバイナリエディタで開いてみたものです。選択されている先頭44バイトがヘッダ情報で、残りが実際の音声データになっています。
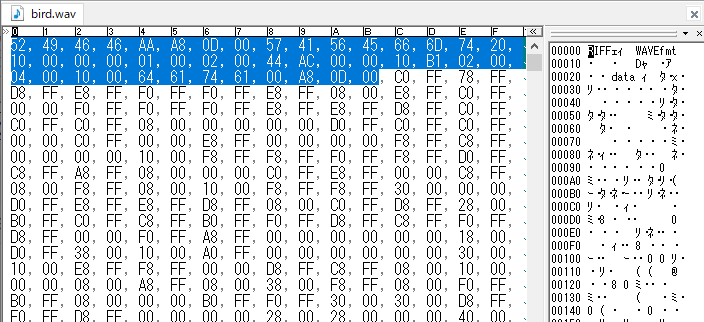
図13:Waveファイルのバイナリ情報
Waveファイルの他にMP3という形式も音声の保存にはよく使われます。MP3は音データを周波数データに分解し、人間の聴覚特性に照らして不要な成分を取り除いてデータサイズを大幅に圧縮します。(MP3がどうやって圧縮をしているかは、この連載の中で触れたいと思います)
こちらも是非
“もっと見る” ブログ
はじめての耐量子暗号
量子コンピューティングはさまざまな面で明るい未来のために期待される技術である反面、その演算能力をセキュリティ上の攻撃に使われることを考えると、既存の暗号技術にとって深刻な脅威でもあります。
Arm®対応のWindows IoT OS 【Windows IoT on Arm】を評価ボードで動かしてみる
組み込み機器向けOS、Windows 10/11 IoT Enterprise(以下Windows IoT)がサポートするArmプラットフォームが拡大しています。Windows IoT on Armは、Windows IoTのメリットそのまま、より低コストで低消費電力というArmならではのメリットもございます
【フーリエ級数からフーリエ変換へ:フーリエ変換編1】イメージでしっかりつかむ信号処理〜基礎から学ぶFFT〜
ここまで学んできたフーリエ級数展開は、「入力信号が周期波形でなければならない」という制約がありました。上図のような太鼓の音、すなわち単発波形は、フーリエ級数展開できないのでしょうか