高校数学最後の壁?微分積分
大学数学の世界は「幾何学」「代数学」「解析学」の3つにざっくり分けることができます。このうち「幾何学」はいわゆる図形分野の知識、「代数学」は式の変形や方程式の知識を問うものであり、どちらも小学校の算数から始まって少しずつコツコツと、時間をかけて知識を身につけていきます。
一方、「解析学」というのは微分・積分(両者をあわせてよく微積分といいます)を基礎とした数学の世界なのですが、微積分という言葉が学校教育の中で最初に登場するのは、高校の「数学II」です。「数学II」の最後のあたりで微積分のごくごく入門部分だけを学び、「数学III」から本格的に学び始めます。長い時間をかけて積み上げた「幾何学」「代数学」に比べると、「解析学」の内容はびっくり箱が飛び出すかのごとく、高校の後半から突然現れてくる印象があります。そのため苦手意識のある人も多いようです。高校数学最後の壁といってもいいでしょう。

図1:大学数学の三大柱「幾何学」「代数学」「解析学」
微積が苦手だと思う人が多い理由は2つあると私は思っています。
一つ目は上で書いた通り「微積という概念が高校で突然現れる《ように見える》」からです。どういう事かというと、微積分とは、それまでに学んできた「変化の割合」とか「図形の面積・体積」とか「距離変化から速度を求める」等といった具体的な計算を、抽象化したものだからです。つまり、微積分という概念が突然出てきたのではなく、個別具体的な計算スキルを小学校から高校前半まで積み上げてきた上で、初めてそれらを統合して一段上の領域に抽象化した時、はじめて微積分という概念に到着するのです。ですから、微積分という概念は決して、何もないところから突然湧き上がる概念ではなく、ちゃんと小学校から積み上げてきた内容の延長線上にあるのですが、その関係性が見えにくいのが理由の一つです。
二つ目の理由は、「微分・積分」という呼び名にも表れている通り、ほとんどの教科書が「微分→積分の順番に学ぶ」からです。微分と積分を比べると、微分は「目に見える大きな〈固まり〉を目に見えないほど薄く細かく分解する」処理なのに対し、積分は「目に見えない小さなものを、目に見える大きさの〈固まり〉になるまでかき集めてくる」処理です。そのため、目に見える〈固まり〉が結果として得られる積分の方が直観的に理解しやすいのですが、微分の方から学ぶという慣例が出来てしまっているため、わざわざ難しい方から勉強してしまっている…と私は考えています。
微分と積分、どちらが大切かと言われればどちらも大切なのですが、幸いにして、本連載の目的であるフーリエ分析の理解をすることだけを考えれば、使用するのは比較的わかりやすい積分の知識が中心です。ですので、本記事では積分の説明を中心に行います。
積分入門のさらに前 総和記号Σ
積分について確認する前に、総和記号Σ(シグマ)についておさらいしておきましょう。文字通り「総て(すべて)の和」を求めるという記号ですが、これは連続信号における積分を離散信号の世界に持ってきた処理に相当します。
プログラムの経験がある人ならば、Σの役割を理解する事は簡単です。Forループ(指定回数繰返し)によって、数値の合計を求める(ことを意味している)だけだからです。図に、総和記号の例と、この計算に相当するプログラム(C言語及びPython)を掲載しています。
プログラムの経験がある人はこの図を見るだけで総和記号の使いかたは分かると思うので、そういう方は次節まで飛ばして頂いても大丈夫です。ただし1か所だけ気を付けて頂きたいのは、繰返しのプログラムを作る時、ループ変数範囲の終了条件の数値(図では100)を「含まない」ように書くことが多いですが、総和記号Σの場合は終了条件の数値を「含む」ことが要注意点です。したがって、図のプログラムでは、上限値に1を足して101にしています。
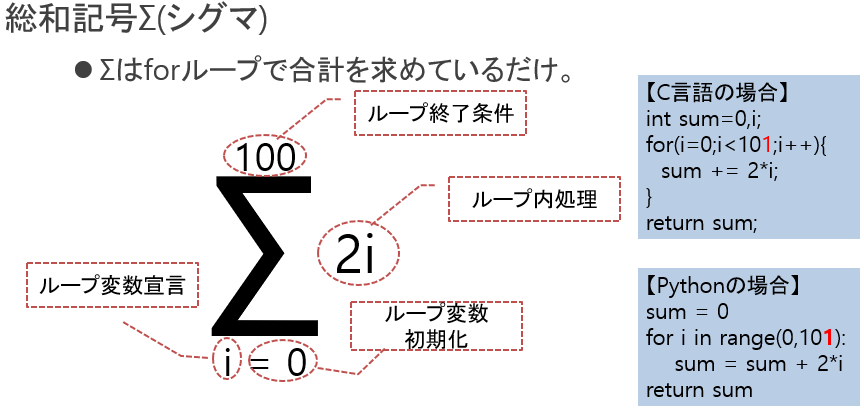
図2:総和記号の使いかた
総和記号は繰り返し処理なので、繰返し関数を管理するための変数(ループ変数)が必要です。Σの下部は「ループ変数の宣言」と「ループ変数の初期化」を示していて、ループ変数に何の記号を使うのか、そしてその初期値をいくつにするのかを表します。
Σの上部は「ループ終了条件」を表します。ループ変数が初期値からはじまり、ループ変数の値を+1しながらこの終了条件に達するまで繰り返し「ループ内処理」を行い、その合計を求めます。(終了条件に示されている数字自身も含まれることに注意して下さい)
上図の総和計算を実施すると、10100という結果が得られます。
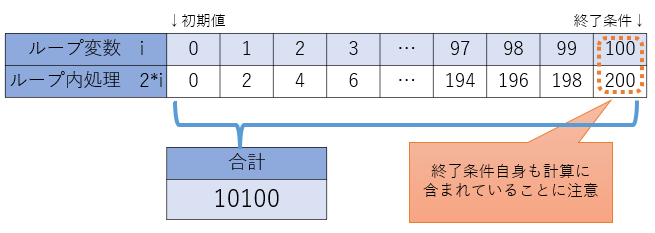
図3:総和計算の例
ちょっと余談:総積(総乗)記号Π
総和記号Σ(シグマ)と同様に、forループで全体の積を求める記号Π(パイ)も存在します。
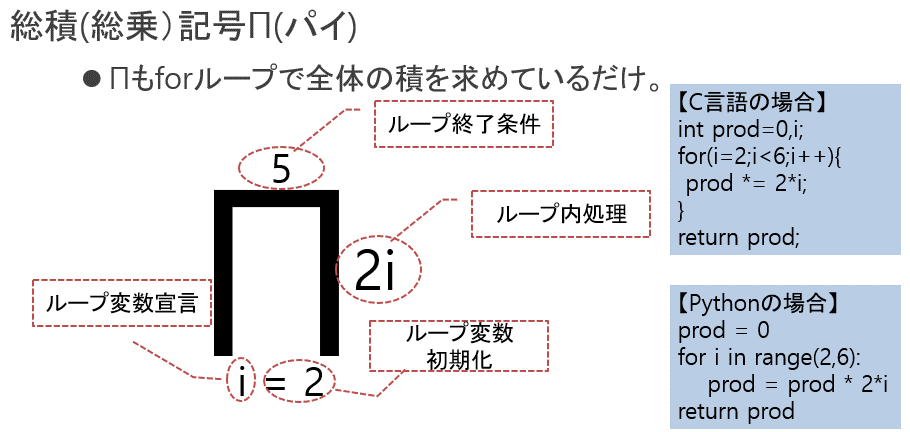
図4:総積(総乗)記号の使いかた
ちなみになぜ総和記号と相乗記号にΣ・Πという記号が選ばれたかというと、合計=SumのSをギリシャ文字にしたものがΣ、積=ProductのPをギリシャ文字にしたものがΠだから、といわれています。
積分と微分
積分と微分は逆演算の関係
積分と微分はお互いに逆演算の関係にあります。
積分は、瞬間瞬間の小さな変化をたくさん積み上げて、全体量(先述の言い方でいえば〈固まり〉)を求める計算です。逆に微分は、全体量(〈固まり〉)を極限まで細かく分割して、隣同士の差を見る事で、「値の変化量(どの程度の激しさで値が変化しているか)」を求める計算です。
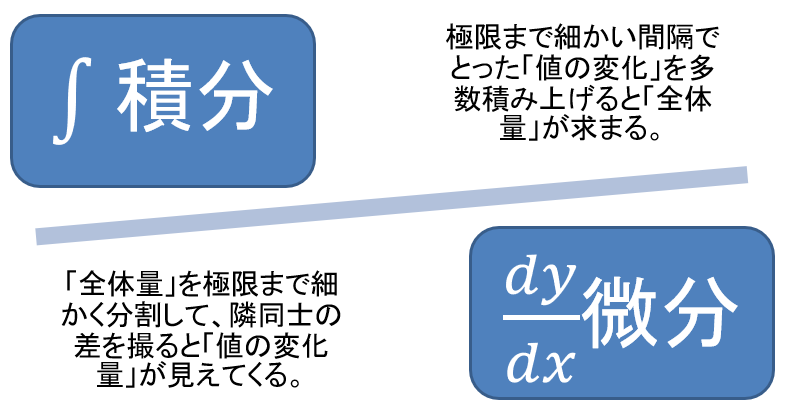
図5:積分と微分
総和記号Σは、ループ変数の値を+1しながら全体の値を合計する計算でしたが、その1回1回の変化幅がごく小さくなったものが積分と思ってください。
体積の計算を通じて積分のイメージをつかむ
直観的に理解しやすい積分計算の例として、体積を求める計算を考えてみましょう。外側の直径が12[cm]、芯の直径が4[cm]のトイレットペーパーの体積を求めてみましょう。
(1)単純に体積の公式を使って求める場合
小学校で学ぶ「円柱の体積の公式」を使えば、外側の円柱体積から芯の円柱体積を引くことで、答えを求めることができます。
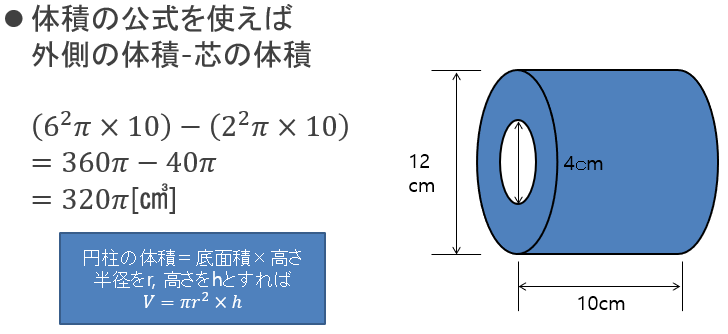
図6:体積の公式を使ってトイレットペーパーの体積を求める
(2)積分の考え方を使い、ドーナツ型を積み上げる場合
トイレットペーパーの形を、極限まで薄く切り取ったドーナツ型が積み上げられた形ととらえてみます。
ドーナツ形の断面積は外形の円(直径12[cm])の面積から芯の円(直径4[cm])を引いて32π[cm2]です。

図7:トイレットペーパーの体積を求めるために、ドーナツ型の面積を求める
厚みが無視できるほど十分に薄い場合、この面積はドーナツ形1枚の体積に相当する値になります(ここはちょっと混乱する人がいるかもしれません。厚みが十分に薄いとして、この厚さが例えば±1%くらい変化したところで体積に影響はありませんが、ドーナツ形の面積を決める12[cm]とか6[cm]という値が±1%変化したら大きな変化になります。「(厚みが十分薄いと)断面積が体積に相当する)というのは、厚みの変化に対して断面積の変化の方がはるかに支配的、と考えるとわかりやすいでしょう)。
このドーナツ形の断面(積)を高さ方向に積み上げて体積を求めます。ここで積分の計算を使います。積分の公式については後述しますが、まずは結果だけ見て下さい。公式で求めた値と同じ体積が出てきます。

図8:ドーナツ形を積み上げればトイレットペーパーの体積になる
(3)積分の考え方を使い、紙の輪を積み上げる場合
積分を使ったもう一つ別のアプローチとして、紙の輪を積み上げて計算する方法を試します。
本来のトイレットペーパーは中心から外に向かって渦巻き(らせん)状に紙が巻かれていますが、これを紙の輪(筒)がたくさん重なっている状態に近似して考えてみます(マトリョーシカを想像して下さい)。
一番外側の紙の輪だけを抜き取り、はさみで切り開くと、長方形ができます。長方形の高さはトイレットペーパーの高さと同じ10[cm]、長方形の幅は直径12cmの円周に相当するので12π[cm]です。この長方形の面積は10×12π=120πと簡単に計算できます。
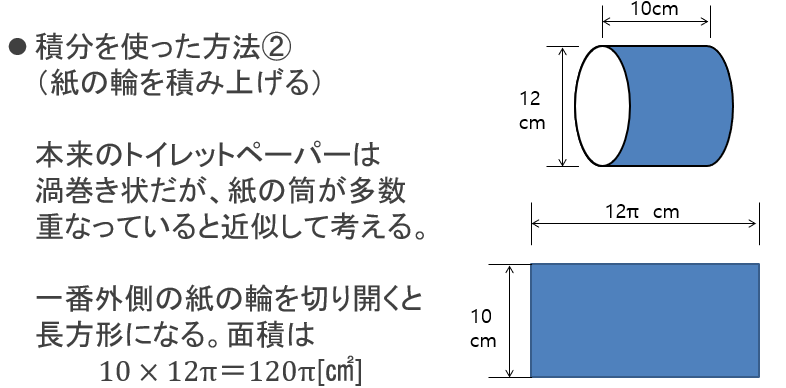
図9:トイレットペーパーの体積を求めるために、紙筒の面積を求める①
さらにその内側にある紙の輪を考えると、一番外側に比べて、輪の半径が少し小さくなっているはずです。この少し小さくなった半径をr[cm]とすれば、この輪を切り開いた長方形の面積は10×2πr=20πrです。
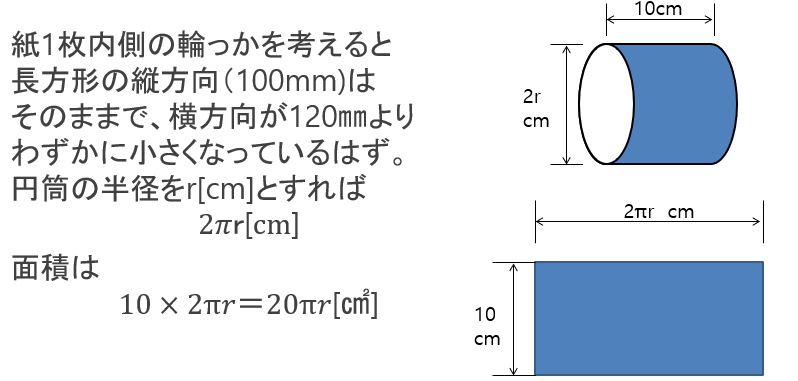
図10:トイレットペーパーの体積を求めるために、紙筒の面積を求める②
芯の直径が4[cm](=半径2[cm])、トイレットペーパーの外形が直径12[cm] (=半径6[cm])なので、rを4[cm]~6[cm]の範囲でほんのわずかずつ変化さえながら積み重ねていけば、トイレットペーパーの体積が求められるはずです。実際に計算してみると、やはり同じ結果が得られます。

図11:紙筒を隙間なく並べればトイレットペーパーの体積になる
最低限チェックしておいて欲しい積分の公式
不定積分
積分と微分はお互いに逆関数の関係にあると言いましたが、より正確に言えば微分の逆関数になるのは「不定積分」という計算です。これからの学習をするにあたって、積分の記号が示す意味と、最低限の公式をチェックしておきましょう。
積分は、Σを縦に引き伸ばしたような記号(∫:インテグラル)で書きます。そしてΣと違い、後ろにd●という記号が付くことも特徴です。これは、∫とd●で挟まれた式を、変数●を変化させて積分する、という意味になります。

図12:不定積分と定積分
最低限チェックしておいて欲しい不定積分の公式を以下に示します。

表1:主要な不定積分の公式
積分定数Cというものが突然出てきますが、これは不定積分をするときに出てくるおまけのようなものです。不定積分は微分の逆関数、すなわち「微分をすると元の形(∫の中身)に戻る式」を求める手続きでしたが、このCの中にはどんな実数が入っても、微分をするとまた元の形に戻ります。そのような式全体を表すために積分定数という定数項をつけるのです。(関数の初期値など付属条件が付く場合には、Cの値が具体的に確定することもあります。)
指数関数の不定積分は特別な形をしていますね。積分をした後も全く同じ形をしています。(積分定数Cはつきますが)。前々回の記事で、自然対数の底(ネイピア数)は「微分をしても形が変わらない指数関数を作るような、対数の底」と説明しました。積分と微分は逆関数の関係なので、微分しても形が変わらないということは、逆演算である積分もまた、形が変わらないのです。
定積分
積分計算をする範囲を決めてあげると「定積分」になります。不定積分の公式がわかっていれば、定積分は簡単に求めることができます。先に説明した面積や体積を求める計算はこの定積分の計算に相当します。
定積分はインテグラルの上下に積分範囲の上限と下限が示されています。定積分の結果を求める時は、まず元の関数の不定積分を求めます(ただし、後の引き算で必ず消えてしまうので、積分定数Cは書かなくて良いです)。得られた関数にx=aを代入したものから、x=bを代入したものを引くと、定積分の結果が得られます。
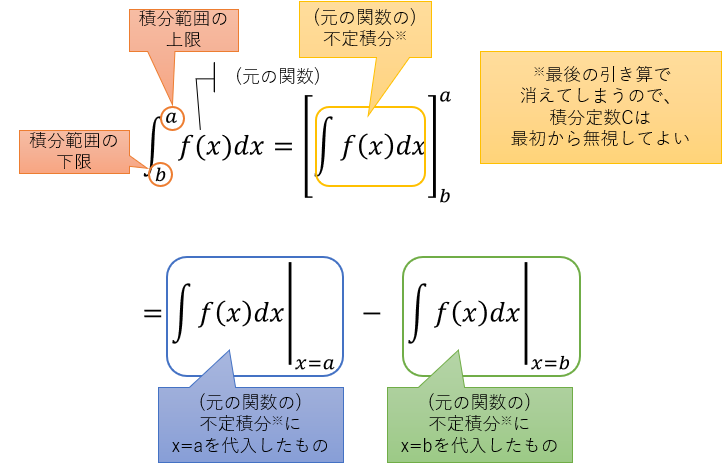
図13:定積分の求め方
練習問題
簡単な練習問題をいくつかやっておきましょう。(どうしても計算はいやだ!という人は飛ばしても構いません。便利なツールを連載の中で紹介します)

図14:積分の練習問題①

図15:積分の練習問題②

図16:積分の練習問題③

図17:積分の練習問題④

図18:積分の練習問題⑤
こちらも是非
“もっと見る” ブログ
はじめての耐量子暗号
量子コンピューティングはさまざまな面で明るい未来のために期待される技術である反面、その演算能力をセキュリティ上の攻撃に使われることを考えると、既存の暗号技術にとって深刻な脅威でもあります。
Arm®対応のWindows IoT OS 【Windows IoT on Arm】を評価ボードで動かしてみる
組み込み機器向けOS、Windows 10/11 IoT Enterprise(以下Windows IoT)がサポートするArmプラットフォームが拡大しています。Windows IoT on Armは、Windows IoTのメリットそのまま、より低コストで低消費電力というArmならではのメリットもございます
【フーリエ級数からフーリエ変換へ:フーリエ変換編1】イメージでしっかりつかむ信号処理〜基礎から学ぶFFT〜
ここまで学んできたフーリエ級数展開は、「入力信号が周期波形でなければならない」という制約がありました。上図のような太鼓の音、すなわち単発波形は、フーリエ級数展開できないのでしょうか














